
如圖所示,一種醫(yī)用輸液瓶可以視為兩個圓柱的組合體.開始輸液時,滴管內(nèi)勻速滴下球狀液體,其中球狀液體的半徑 毫米,滴管內(nèi)液體忽略不計.
毫米,滴管內(nèi)液體忽略不計.
(1)如果瓶內(nèi)的藥液恰好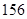 分鐘滴完,問每分鐘應(yīng)滴下多少滴?
分鐘滴完,問每分鐘應(yīng)滴下多少滴?
(2)在條件(1)下,設(shè)輸液開始后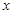 (單位:分鐘),瓶內(nèi)液面與進(jìn)氣管的距離為
(單位:分鐘),瓶內(nèi)液面與進(jìn)氣管的距離為 (單位:厘米),已知當(dāng)
(單位:厘米),已知當(dāng) 時,
時,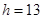 .試將
.試將 表示為
表示為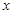 的函數(shù).(注:
的函數(shù).(注: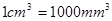 )
)
(1)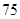 ;(2)
;(2) ;
;
解析試題分析:(1)本小題主要通過題中給出圖形與數(shù)據(jù)求得瓶內(nèi)液體的體積(兩個圓柱體的體積和)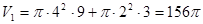
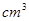 ,再計算
,再計算 滴球狀液體的體積
滴球狀液體的體積
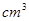 ,然后利用二者相等
,然后利用二者相等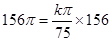 ,求得
,求得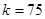 ;
;
(2)本小題任然根據(jù)滴管內(nèi)勻速滴下球狀液體體積等于瓶內(nèi)液體下降的體積,只是需要注意瓶內(nèi)液體應(yīng)區(qū)分兩個圓柱體體積的不同,所以所得為分段函數(shù) 。
。
試題解析:(1)設(shè)每分鐘滴下 (
(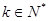 )滴, 1分
)滴, 1分
則瓶內(nèi)液體的體積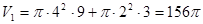
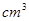 3分
3分 滴球狀液體的體積
滴球狀液體的體積
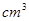 5分
5分
所以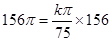 ,解得
,解得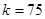 ,故每分鐘應(yīng)滴下
,故每分鐘應(yīng)滴下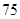 滴。 6分
滴。 6分
(2)由(1)知,每分鐘滴下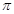
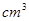 藥液 7分
藥液 7分
當(dāng)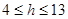 時,
時,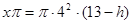 ,即
,即 ,此時
,此時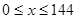 10分
10分
當(dāng)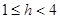 時,
時,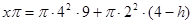 ,即
,即 ,此時
,此時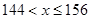 13分
13分
綜上可得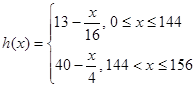 14分
14分
考點(diǎn):1.幾何體體積的計算;2.分段函數(shù).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù)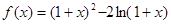
(1)若關(guān)于x的不等式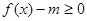 在
在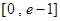 有實數(shù)解,求實數(shù)m的取值范圍;
有實數(shù)解,求實數(shù)m的取值范圍;
(2)設(shè)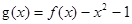 ,若關(guān)于x的方程
,若關(guān)于x的方程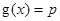 至少有一個解,求p的最小值.
至少有一個解,求p的最小值.
(3)證明不等式: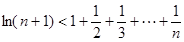
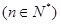
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如果函數(shù) 滿足在集合
滿足在集合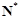 上的值域仍是集合
上的值域仍是集合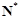 ,則把函數(shù)
,則把函數(shù) 稱為N函數(shù).
稱為N函數(shù).
例如: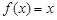 就是N函數(shù).
就是N函數(shù).
(Ⅰ)判斷下列函數(shù):①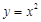 ,②
,②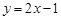 ,③
,③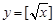 中,哪些是N函數(shù)?(只需寫出判斷結(jié)果);
中,哪些是N函數(shù)?(只需寫出判斷結(jié)果);
(Ⅱ)判斷函數(shù)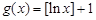 是否為N函數(shù),并證明你的結(jié)論;
是否為N函數(shù),并證明你的結(jié)論;
(Ⅲ)證明:對于任意實數(shù)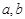 ,函數(shù)
,函數(shù)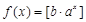 都不是N函數(shù).
都不是N函數(shù).
(注:“ ”表示不超過
”表示不超過 的最大整數(shù))
的最大整數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
經(jīng)市場調(diào)查,某種商品在過去50天的銷售量和價格均為銷售時間t(天)的函數(shù),且銷售量近似地滿足f(t)=-2t+200(1≤t≤50,t∈N).前30天價格為g(t)=t+30(1≤t≤30,t∈N),后20天價格為g(t)=45(31≤t≤50,t∈N).
(1)寫出該種商品的日銷售額S與時間t的函數(shù)關(guān)系;
(2)求日銷售額S的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè) ,兩個函數(shù)
,兩個函數(shù) ,
, 的圖像關(guān)于直線
的圖像關(guān)于直線 對稱.
對稱.
(1)求實數(shù) 滿足的關(guān)系式;
滿足的關(guān)系式;
(2)當(dāng) 取何值時,函數(shù)
取何值時,函數(shù) 有且只有一個零點(diǎn);
有且只有一個零點(diǎn);
(3)當(dāng) 時,在
時,在 上解不等式
上解不等式 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
對于函數(shù) ,若存在實數(shù)對(
,若存在實數(shù)對( ),使得等式
),使得等式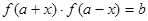 對定義域中的每一個
對定義域中的每一個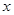 都成立,則稱函數(shù)
都成立,則稱函數(shù) 是“(
是“( )型函數(shù)”.
)型函數(shù)”.
(Ⅰ)判斷函數(shù)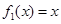 是否為 “(
是否為 “( )型函數(shù)”,并說明理由;
)型函數(shù)”,并說明理由;
(Ⅱ)若函數(shù)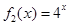 是“(
是“( )型函數(shù)”,求出滿足條件的一組實數(shù)對
)型函數(shù)”,求出滿足條件的一組實數(shù)對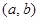 ;,
;,
(Ⅲ)已知函數(shù) 是“(
是“( )型函數(shù)”,對應(yīng)的實數(shù)對
)型函數(shù)”,對應(yīng)的實數(shù)對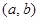 為
為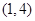 .當(dāng)
.當(dāng)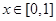 時,
時,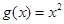
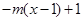
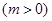 ,若當(dāng)
,若當(dāng)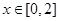 時,都有
時,都有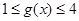 ,試求
,試求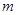 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖是某重點(diǎn)中學(xué)學(xué)校運(yùn)動場平面圖,運(yùn)動場總面積15000平方米,運(yùn)動場是由一個矩形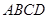 和分別以
和分別以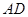 、
、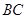 為直徑的兩個半圓組成,塑膠跑道寬8米,已知塑膠跑道每平方米造價為150元,其它部分造價每平方米80元,
為直徑的兩個半圓組成,塑膠跑道寬8米,已知塑膠跑道每平方米造價為150元,其它部分造價每平方米80元,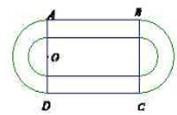
(Ⅰ)設(shè)半圓的半徑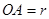 (米),寫出塑膠跑道面積
(米),寫出塑膠跑道面積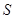 與
與 的函數(shù)關(guān)系式
的函數(shù)關(guān)系式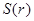 ;
;
(Ⅱ)由于受運(yùn)動場兩側(cè)看臺限制, 的范圍為
的范圍為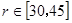 ,問當(dāng)
,問當(dāng) 為何值時,運(yùn)動場造價最低(第2問
為何值時,運(yùn)動場造價最低(第2問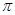 取3近似計算).
取3近似計算).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com