解:(I)設助跑道所在的拋物線方程為f(x)=a
0x
2+b
0x+c
0,
由題意知
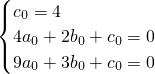
解得a
0=1,b
0=-4,c
0=4,
∴助跑道所在的拋物線方程為y=x
2-4x+4.
(II)設飛行軌跡所在拋物線方程為g(x)=ax
2+bx+c,(a<0)
由題意知
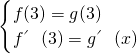
,得
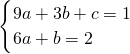
,解得
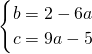
∴g(x)=ax
2+(2-6a)x+9a-5=a(x-
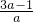
)
2+1-

,
令g(x)=1,得(x-
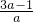
)
2=

,
∵a<0,∴x=
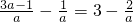
,
當x=
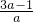
時,g(x)有最大值1-

,
則運動員飛行距離d=3-

-3=-

,飛行過程中距離平臺最大高度h=1-

-1=-

,
依題意4≤-

≤6,得2≤-

≤3.
飛行過程中距離平臺最大高度的取值范圍在2米到3米之間.
分析:(1)設助跑道所在的拋物線方程為f(x)=a
0x
2+b
0x+c
0,由題意,助跑道一端點A(0,4),另一端點C(3,1),點B(2,0),得出方程組,由此能求出結果.
(2)設飛行軌跡所在拋物線方程為g(x)=ax
2+bx+c,(a<0),由題意知
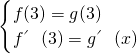
,由此入手能求出g(x)有最大值,用飛行過程中距離平臺最大高度,利用不等關系即可得出運動員飛行過程中距離平臺最大高度的取值范圍.
點評:本題考查拋物線方程的求法,考查滿足條件的實數的取值范圍的求法,解題時要認真審題,仔細解答,注意等價轉化思想的合理運用.

 輪滑是穿著帶滾輪的特制鞋在堅硬的場地上滑行的運動.如圖,助跑道ABC是一段拋物線,某輪滑運動員通過助跑道獲取速度后飛離跑道然后落到離地面高為1米的平臺上E處,飛行的軌跡是一段拋物線CDE(拋物線CDE與拋物線ABC在同一平面內),D為這段拋物線的最高點.現在運動員的滑行軌跡所在平面上建立如圖所示的直角坐標系,x軸在地面上,助跑道一端點A(0,4),另一端點C(3,1),點B(2,0),單位:米.
輪滑是穿著帶滾輪的特制鞋在堅硬的場地上滑行的運動.如圖,助跑道ABC是一段拋物線,某輪滑運動員通過助跑道獲取速度后飛離跑道然后落到離地面高為1米的平臺上E處,飛行的軌跡是一段拋物線CDE(拋物線CDE與拋物線ABC在同一平面內),D為這段拋物線的最高點.現在運動員的滑行軌跡所在平面上建立如圖所示的直角坐標系,x軸在地面上,助跑道一端點A(0,4),另一端點C(3,1),點B(2,0),單位:米.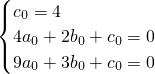
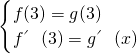 ,得
,得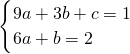 ,解得
,解得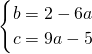
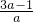 )2+1-
)2+1- ,
,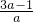 )2=
)2= ,
,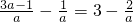 ,
,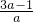 時,g(x)有最大值1-
時,g(x)有最大值1- ,
, -3=-
-3=- ,飛行過程中距離平臺最大高度h=1-
,飛行過程中距離平臺最大高度h=1- -1=-
-1=- ,
, ≤6,得2≤-
≤6,得2≤- ≤3.
≤3.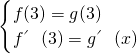 ,由此入手能求出g(x)有最大值,用飛行過程中距離平臺最大高度,利用不等關系即可得出運動員飛行過程中距離平臺最大高度的取值范圍.
,由此入手能求出g(x)有最大值,用飛行過程中距離平臺最大高度,利用不等關系即可得出運動員飛行過程中距離平臺最大高度的取值范圍.

 某幾何體的一條棱長為
某幾何體的一條棱長為 “5•12”汶川大地震是華人心中永遠的痛!在災后重建中擬在矩形區域ABCD內建一矩形(與原方位一樣)的汶川人民紀念廣場(如圖),另外AEF內部有一廢墟作為文物保護區不能占用,經測量AB=100m,BC=80m,AE=30m,AF=20m,如何設計才能使廣場面積最大?
“5•12”汶川大地震是華人心中永遠的痛!在災后重建中擬在矩形區域ABCD內建一矩形(與原方位一樣)的汶川人民紀念廣場(如圖),另外AEF內部有一廢墟作為文物保護區不能占用,經測量AB=100m,BC=80m,AE=30m,AF=20m,如何設計才能使廣場面積最大?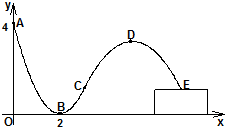 輪滑是穿著帶滾輪的特制鞋在堅硬的場地上滑行的運動.如圖,助跑道ABC是一段拋物線,某輪滑運動員通過助跑道獲取速度后飛離跑道然后落到離地面高為1米的平臺上E處,飛行的軌跡是一段拋物線CDE(拋物線CDE與拋物線ABC在同一平面內),D為這段拋物線的最高點.現在運動員的滑行軌跡所在平面上建立如圖所示的直角坐標系,x軸在地面上,助跑道一端點A(0,4),另一端點C(3,1),點B(2,0),單位:米.
輪滑是穿著帶滾輪的特制鞋在堅硬的場地上滑行的運動.如圖,助跑道ABC是一段拋物線,某輪滑運動員通過助跑道獲取速度后飛離跑道然后落到離地面高為1米的平臺上E處,飛行的軌跡是一段拋物線CDE(拋物線CDE與拋物線ABC在同一平面內),D為這段拋物線的最高點.現在運動員的滑行軌跡所在平面上建立如圖所示的直角坐標系,x軸在地面上,助跑道一端點A(0,4),另一端點C(3,1),點B(2,0),單位:米.