
【題目】已知函數![]() .
.
(1)若![]() 為奇函數,求
為奇函數,求![]() 的值;
的值;
(2)試判斷![]() 在
在![]() 內的單調性,并用定義證明.
內的單調性,并用定義證明.
【答案】(1)1(2)見解析
【解析】試題分析:(1)![]() ,由于函數
,由于函數![]() 為奇函數,所以有
為奇函數,所以有![]() ,即
,即![]() ,解得
,解得![]() ;(2)首先判斷函數
;(2)首先判斷函數![]() 在區間
在區間![]() 上單調遞增,可以根據函數單調性定義進行證明,設
上單調遞增,可以根據函數單調性定義進行證明,設![]() 是區間
是區間![]() 上任意兩個不等的實數,且
上任意兩個不等的實數,且![]() ,則
,則![]() ,
, 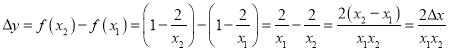 ,由于
,由于![]() 且
且![]() ,所以
,所以![]() ,即
,即![]() ,所以函數
,所以函數![]() 在區間
在區間![]() 上單調遞增.
上單調遞增.
試題解析:(1)由已知g(x)=f(x)-a得,
g(x)=1-a-![]() ,
,
因為g (x)是奇函數,所以g(-x)=-g(x),
即1-a-![]() =-
=-![]() ,
,
解得a=1.
(2)函數f(x)在(0,+∞)內為增函數.
證明如下:
設x1、x2為(0,+∞)內的任意兩點,且x1<x2,
則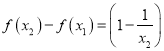
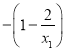
![]() .
.
因為0<x1<x2,所以![]() ,x1x2>0,
,x1x2>0,
從而![]() ,
,
即f(x1)<f(x2).
所以函數f(x)在(0,+∞)內是增函數.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】解答下列問題:
(1)求平行于直線3x+4y- 2=0,且與它的距離是1的直線方程;
(2)求垂直于直線x+3y -5=0且與點P( -1,0)的距離是![]() 的直線方程.
的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是R上的奇函數,當x>0時,解析式為f(x)=![]() .
.
(1)求f(x)在R上的解析式;
(2)用定義證明f(x)在(0,+∞)上為減函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究型學習小組調查研究高中生使用智能手機對學習的影響,部分統計數據如下:
使用智能手機 | 不使用智能手機 | 合計 | |
學習成績優秀 |
|
| |
學習成績不優秀 |
|
| |
合計 |
(1)根據以上統計數據,你是否有![]() 的把握認為使用智能手機對學習有影響?
的把握認為使用智能手機對學習有影響?
(2)為進一步了解學生對智能手機的使用習慣,現從全校使用智能手機的高中生中(人數很多)隨機抽取 ![]() 人,求抽取的學生中學習成績優秀的與不優秀的都有的概率.
人,求抽取的學生中學習成績優秀的與不優秀的都有的概率.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三名工人加工同一種零件,他們在一天中的工作情況如圖所示,其中Ai的橫、縱坐標分別為第i名工人上午的工作時間和加工的零件數,點Bi的橫、縱坐標分別為第i名工人下午的工作時間和加工的零件數,i=1,2,3.
①記Qi為第i名工人在這一天中加工的零件總數,則Q1 , Q2 , Q3中最大的是 .
②記pi為第i名工人在這一天中平均每小時加工的零件數,則p1 , p2 , p3中最大的是 . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知y=f(x)是定義在R上的偶函數,當x![]() 0時,f(x)=
0時,f(x)=![]() .
.
(1)求當x<0時,f(x)的解析式;
(2)作出函數f(x)的圖象,并指出其單調區間.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市要對該市六年級學生進行體育素質調查測試,現讓學生從“跳繩、短跑![]() 米、長跑
米、長跑![]() 米、仰臥起坐、游泳
米、仰臥起坐、游泳![]() 米、立定跳遠”
米、立定跳遠”![]() 項中選擇
項中選擇![]() 項進行測試,其中“短跑、長跑、仰臥起坐”
項進行測試,其中“短跑、長跑、仰臥起坐”![]() 項中至少選擇其中
項中至少選擇其中![]() 項進行測試.現從該市六年級學生中隨機抽取了
項進行測試.現從該市六年級學生中隨機抽取了![]() 名學生進行調查,他們選擇的項目中包含“短跑、長跑、仰臥起坐”的項目個數及人數統計如下表:(其中
名學生進行調查,他們選擇的項目中包含“短跑、長跑、仰臥起坐”的項目個數及人數統計如下表:(其中![]() )
)
選擇的項目中包含“短跑、長跑、仰臥起坐”的項目個數 |
|
|
|
人數 |
|
|
|
已知從所調查的![]() 名學生中任選
名學生中任選![]() 名,他們選擇“短跑、長跑、仰臥起坐”的項目個數不相等概率為
名,他們選擇“短跑、長跑、仰臥起坐”的項目個數不相等概率為![]() ,記
,記![]() 為這
為這![]() 名學生選擇“短跑、長跑、仰臥起坐”的項目個數之和.
名學生選擇“短跑、長跑、仰臥起坐”的項目個數之和.
(1)求![]() 的值;
的值;
(2)求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙曲線E: ![]() =1(a>0,b>0)的左、右焦點分別為F1、F2 , P是E坐支上一點,且|PF1|=|F1F2|,直線PF2與圓x2+y2=a2相切,則E的離心率為 .
=1(a>0,b>0)的左、右焦點分別為F1、F2 , P是E坐支上一點,且|PF1|=|F1F2|,直線PF2與圓x2+y2=a2相切,則E的離心率為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,鄭州經濟快速發展,躋身新一線城市行列,備受全國矚目.無論是市內的井字形快速交通網,還是輻射全國的米字形高鐵路網,鄭州的交通優勢在同級別的城市內無能出其右.為了調查鄭州市民對出行的滿意程度,研究人員隨機抽取了1000名市民進行調查,并將滿意程度以分數的形式統計成如下的頻率分布直方圖,其中![]() .
.

(I)求![]() 的值;
的值;
(Ⅱ)求被調查的市民的滿意程度的平均數,眾數,中位數;
(Ⅲ)若按照分層抽樣從![]() ,
,![]() 中隨機抽取8人,再從這8人中隨機抽取2人,求至少有1人的分數在
中隨機抽取8人,再從這8人中隨機抽取2人,求至少有1人的分數在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com