
【題目】已知函數![]() ,
, ![]() 在
在![]() 和
和![]() 處取得極值,且
處取得極值,且![]() ,曲線
,曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 垂直.
垂直.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)證明關于![]() 的方程
的方程![]() 至多只有兩個實數根(其中
至多只有兩個實數根(其中![]() 是
是![]() 的導函數,
的導函數, ![]() 是自然對數的底數).
是自然對數的底數).
【答案】(Ⅰ)![]() (Ⅱ)見解析.
(Ⅱ)見解析.
【解析】試題分析:(Ⅰ)先求![]() ,根據韋達定理及
,根據韋達定理及![]() 列出關于
列出關于![]() 的方程組,進而可得結果;(Ⅱ)圓方程等價于
的方程組,進而可得結果;(Ⅱ)圓方程等價于![]() ,令
,令![]() ,研究函數
,研究函數![]() 的單調性,討論
的單調性,討論![]() 與
與![]() 兩種情況分別證明即可.
兩種情況分別證明即可.
試題解析:(Ⅰ) ![]() ,因為
,因為![]() 在
在![]() 和
和![]() 處取得極值,
處取得極值,
所以![]() 和
和![]() 是方程
是方程![]() 的兩個根,則
的兩個根,則![]() ,
, ![]() ,
,
又![]() ,則
,則![]() ,所以
,所以![]() .
.
由已知曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 垂直,所以可得
垂直,所以可得![]() ,
,
即![]() ,由此可得
,由此可得![]() 解得
解得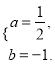
所以![]()
(Ⅱ)對于![]() ,
,
(1)當![]() 時,得
時,得![]() ,方程無實數根;
,方程無實數根;
(2)當![]() 時,得
時,得![]() ,令
,令![]() ,
,
![]()
![]() ,
,
當![]() 時,
時, ![]() ;
;
當![]() 或
或![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
∴![]() 的單調遞減區間是
的單調遞減區間是![]() 和
和![]() ,單調遞增區間是
,單調遞增區間是![]() ,
,
函數![]() 在
在![]() 和
和![]() 處分別取得極小值和極大值.
處分別取得極小值和極大值.
![]() ,
, ![]() ,
,
對于![]() ,由于
,由于![]() 恒成立,
恒成立,
且![]() 是與
是與![]() 軸有兩個交點、開口向上的拋物線,
軸有兩個交點、開口向上的拋物線,
所以曲線![]() 與
與![]() 軸有且只有兩個交點,從而
軸有且只有兩個交點,從而![]() 無最大值,
無最大值, ![]() .
.
若![]() 時
時![]()
![]() ,直線
,直線![]() 與曲線
與曲線![]() 至多有兩個交點;
至多有兩個交點;
若![]()
![]()
![]() ,直線
,直線![]() 與曲線
與曲線![]() 只有一個交點;
只有一個交點;
綜上所述,無論![]() 取何實數,方程
取何實數,方程![]() 至多只有兩實數根.
至多只有兩實數根.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的左,右頂點分別為
的左,右頂點分別為![]() .過點
.過點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() 的面積的3倍.
的面積的3倍.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 與
與![]() 軸垂直,
軸垂直,![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的動點,且滿足
兩側的動點,且滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值,請說明理由.
的斜率是否為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側面ABB1A1 , ACC1A1均為正方形,AB=AC=1,∠BAC=90,點D是棱B1C1的中點. 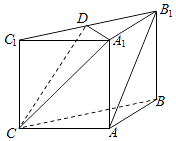
(1)求證:AB1∥平面A1DC;
(2)求證:A1D⊥平面BB1C1C.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司2016年前三個月的利潤(單位:百萬元)如下:
月份 | 1 | 2 | 3 |
利潤 | 2 | 3.9 | 5.5 |
(1)求利潤![]() 關于月份
關于月份![]() 的線性回歸方程;
的線性回歸方程;
(2)試用(1)中求得的回歸方程預測4月和5月的利潤;
(3)試用(1)中求得的回歸方程預測該公司2016年從幾月份開始利潤超過1000萬?
相關公式: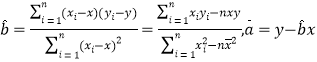 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點 ,順次連接橢圓的四個頂點得到的四邊形的面積為
,順次連接橢圓的四個頂點得到的四邊形的面積為![]() ,點
,點![]() .
.
(Ⅰ)求橢圓![]() 的方程.
的方程.
(Ⅱ)已知點![]() ,是橢圓
,是橢圓![]() 上的兩點.
上的兩點.
(ⅰ)若![]() ,且
,且![]() 為等邊三角形,求
為等邊三角形,求![]() 的面積;
的面積;
(ⅱ)若![]() ,證明:
,證明: ![]() 不可能為等邊三角形.
不可能為等邊三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答題
(1)在等比數列{an}中,a5=162,公比q=3,前n項和Sn=242,求首項a1和項數n.
(2)有四個數,其中前三個數成等比數列,其積為216,后三個數成等差數列,其和為36,求這四個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() :
: ![]() ,曲線
,曲線![]() :
: ![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(Ⅰ)求曲線![]() ,
, ![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)曲線![]() :
: ![]() (
(![]() 為參數,
為參數, ![]() ,
, ![]() )分別交
)分別交![]() ,
, ![]() 于
于![]() ,
, ![]() 兩點,當
兩點,當![]() 取何值時,
取何值時, ![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,與
,與![]() 軸的正半軸交于點
軸的正半軸交于點![]() ,右焦點
,右焦點![]() ,
, ![]() 為坐標原點,且
為坐標原點,且![]() .
.
(1)求橢圓的離心率![]() ;
;
(2)已知點![]() ,過點
,過點![]() 任意作直線
任意作直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,設直線
兩點,設直線![]() 的斜率
的斜率![]() ,若
,若![]() ,求橢圓
,求橢圓![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com