【題目】某商人投資81萬元建一間工作室，第一年裝修費為1萬元，以后每年增加2萬元，把工作室出租，每年收入租金30萬元．
(1)若扣除投資和各種裝修費，則從第幾年開始獲取純利潤？
(2)若干年后該商人為了投資其他項目，對該工作室有兩種處理方案：①年平均利潤最大時，以46萬元出售該工作室；②純利潤總和最大時，以10萬元出售該工作室．問該商人會選擇哪種方案？
【答案】（1）從第4年開始獲取純利潤。
（2）兩種方案獲利一樣多，而方案（1）時間比較短，所以選擇方案（1）。
【解析】試題分析：（1）設第n年獲取利潤為y萬元，n年共收入租金30n萬元．付出裝修費共
，付出投資81萬元，由此可知利潤y=30n-（81+n2），由y＞0能求出從第幾年開始獲取純利潤．
（2）①純利潤總和最大時，以10萬元出售，利用二次函數的性質求出最大利潤，方案②利用基本不等式進行求解，當兩種方案獲利一樣多，就看時間哪個方案短就選擇哪個．.
（1）設第
年獲取利潤為
萬元。………………1分
年共收租金30萬元，付出裝修費構成一個以1為首項，2為公差的等差數列，
共
…………………2分
因此利潤
令
……………4分
解得
……………5分
所以從第4年開始獲取純利潤。………………6分
（2）年平均利潤
………………8分
………………9分
（當且僅當
）所以9年后共獲利潤：154萬元。……………10分
利潤
所以15年后共獲利潤：144+10=154萬元……………………11分
兩種方案獲利一樣多，而方案（1）時間比較短，所以選擇方案（1）。…………………12分
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn，且滿足a1=2，Sn-4Sn-1-2=0（n≥2，n∈Z）．
（Ⅰ）求數列{an}的通項公式；
（Ⅱ）令bn=log2an，Tn為{bn}的前n項和，求證
＜2．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四邊形ABCD中，AB⊥AD，AD∥BC，AD＝6，BC＝2AB＝4，E，F分別在BC，AD上，EF∥AB.現將四邊形ABCD沿EF折起，使平面ABEF⊥平面EFDC.
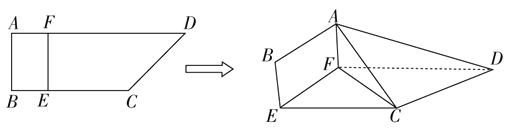
（Ⅰ）若BE＝1，是否在折疊后的線段AD上存在一點P，且
，使CP∥平面ABEF？若存在，求出λ的值，若不存在，說明理由；
（Ⅱ）求三棱錐A－CDF的體積的最大值，并求出此時二面角E－AC－F的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知復數z在復平面內對應的點在第四象限，且z是方程x2﹣4x+5=0的根．
（1）求復數z；
（2）復數w=a﹣ 
（a∈R）滿足|w﹣z|＜2 
，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2+2ax+a+1．
（1）當a=1時，求函數在區間[﹣2，3]上的值域；
（2）函數f（x）在[﹣5，5]上單調，求實數a的取值范圍；
（3）求函數f（x）在[0，2]上的最小值g（a）的解析式．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝
＋aln x(a≠0，a∈R)．
(1)若a＝1，求函數f(x)的極值和單調區間；
(2)若在區間(0，e]上至少存在一點x0，使得f(x0)<0成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
（1）當x≤0時，解不等式f（x）≥﹣1；
（2）寫出該函數的單調區間；
（3）若函數g（x）=f（x）﹣m恰有3個不同零點，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知復數z=（2m2+3m﹣2）+（m2+m﹣2）i，（m∈R）根據下列條件，求m值．
（1）z是實數；
（2）z是虛數；
（3）z是純虛數；
（4）z=0．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數f（x）定義域中任意的x1 ， x2（x1≠x2）有如下結論
1）f（x1+x2）=f（x1）f（x2）
2）f（x1x2）=f（x1）+f（x2）
3） 
＞0
4）f（ 
）＜ 
5）f（ ）＞
6）f（﹣x）=f（x）．
當f（x）=lgx時，上述結論正確的序號為 ． （注：把你認為正確的命題的序號都填上）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com