
【題目】已知函數![]() ,有下列四個結論:
,有下列四個結論:
①![]() 為偶函數;②
為偶函數;②![]() 的值域為
的值域為![]() ;
;
③![]() 在
在![]() 上單調遞減;④
上單調遞減;④![]() 在
在![]() 上恰有8個零點,
上恰有8個零點,
其中所有正確結論的序號為( )
A.①③B.②④C.①②③D.①③④
【答案】A
【解析】
由偶函數的定義可判斷①正確,借助二倍角公式將函數化簡為 利用二次函數性質計算可得②錯誤,利用復合函數的單調性可判斷
利用二次函數性質計算可得②錯誤,利用復合函數的單調性可判斷![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]() ,則
,則![]() 在
在![]() 上單調遞增,根據偶函數性質可得出③正確,利用函數與方程的思想解方程即可判斷④錯誤.
上單調遞增,根據偶函數性質可得出③正確,利用函數與方程的思想解方程即可判斷④錯誤.
由![]() ,故
,故![]() 為偶函數,①正確;
為偶函數,①正確; ,
,
記![]() ,則
,則 ,
,
當![]() 時,
時,![]() 取得最大值2,當
取得最大值2,當![]() 時,
時,![]() 取9得最小值
取9得最小值![]() ,
,
即 的值域為
的值域為![]() ,所以
,所以![]() 的值域為
的值域為![]() ,②錯誤;
,②錯誤;
![]() 在
在![]() 上的單調性與它在
上的單調性與它在![]() 上的單調性剛好相反,
上的單調性剛好相反,
當![]() 時,
時,![]() 單調遞增,且
單調遞增,且 ,而
,而 在
在 時單調遞減,
時單調遞減,
故![]() 在
在![]() 上單調遞減,又此時
上單調遞減,又此時 ,故函數
,故函數![]() 在
在![]() 上單調遞增,于是得
上單調遞增,于是得![]() 在
在![]() 單調遞減,③正確;
單調遞減,③正確;
令![]() ,得
,得![]() 或
或![]() ,而當
,而當![]() 時,
時,![]() 及
及![]() 恰有3個不等的實根
恰有3個不等的實根![]() ,
,![]() ,
,![]() ,
,
即![]() 在區間
在區間![]() 上恰有3個零點,結合奇偶性可知,即
上恰有3個零點,結合奇偶性可知,即![]() 在區間
在區間![]() 上恰有6個零點,④錯誤.
上恰有6個零點,④錯誤.
故正確的是①③.
故選:A.


科目:高中數學 來源: 題型:
【題目】端午節是我國民間為紀念愛國詩人屈原的一個傳統節日.某市為了解端午節期間粽子的銷售情況,隨機問卷調查了該市1000名消費者在去年端午節期間的粽子購買量(單位:克),所得數據如下表所示:
購買量 |
|
|
|
|
|
人數 | 100 | 300 | 400 | 150 | 50 |
將煩率視為概率
(1)試求消費者粽子購買量不低于300克的概率;
(2)若該市有100萬名消費者,請估計該市今年在端午節期間應準備多少千克棕子才能滿足市場需求(以各區間中點值作為該區間的購買量).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業質量檢驗員為了檢測生產線上零件的質量情況,從生產線上隨機抽取了![]() 個零件進行測量,根據所測量的零件尺寸(單位:mm),得到如下的頻率分布直方圖:
個零件進行測量,根據所測量的零件尺寸(單位:mm),得到如下的頻率分布直方圖:
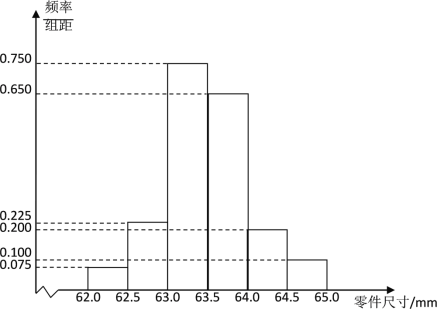
(1)根據頻率分布直方圖,求這![]() 個零件尺寸的中位數(結果精確到
個零件尺寸的中位數(結果精確到![]() );
);
(2)若從這![]() 個零件中尺寸位于
個零件中尺寸位于![]() 之外的零件中隨機抽取
之外的零件中隨機抽取![]() 個,設
個,設![]() 表示尺寸在
表示尺寸在![]() 上的零件個數,求
上的零件個數,求![]() 的分布列及數學期望
的分布列及數學期望![]() ;
;
(3)已知尺寸在![]() 上的零件為一等品,否則為二等品,將這
上的零件為一等品,否則為二等品,將這![]() 個零件尺寸的樣本頻率視為概率. 現對生產線上生產的零件進行成箱包裝出售,每箱
個零件尺寸的樣本頻率視為概率. 現對生產線上生產的零件進行成箱包裝出售,每箱![]() 個. 企業在交付買家之前需要決策是否對每箱的所有零件進行檢驗,已知每個零件的檢驗費用為
個. 企業在交付買家之前需要決策是否對每箱的所有零件進行檢驗,已知每個零件的檢驗費用為![]() 元. 若檢驗,則將檢驗出的二等品更換為一等品;若不檢驗,如果有二等品進入買家手中,企業要向買家對每個二等品支付
元. 若檢驗,則將檢驗出的二等品更換為一等品;若不檢驗,如果有二等品進入買家手中,企業要向買家對每個二等品支付![]() 元的賠償費用. 現對一箱零件隨機抽檢了
元的賠償費用. 現對一箱零件隨機抽檢了![]() 個,結果有
個,結果有![]() 個二等品,以整箱檢驗費用與賠償費用之和的期望值作為決策依據,該企業是否對該箱余下的所有零件進行檢驗?請說明理由.
個二等品,以整箱檢驗費用與賠償費用之和的期望值作為決策依據,該企業是否對該箱余下的所有零件進行檢驗?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點P與點![]() 的距離比它到直線
的距離比它到直線![]() 的距離小1.
的距離小1.
(1)求動點P的軌跡C的方程;
(2)設P為直線![]() 上任一點,過點P作曲線C的切線
上任一點,過點P作曲線C的切線![]() ,
,![]() ,切點分別為A,B,直線
,切點分別為A,B,直線![]() ,
,![]() 與y軸分別交于M,N兩點,點
與y軸分別交于M,N兩點,點![]() 、
、![]() 的縱坐標分別為m,n,求證:m與n的乘積為定值.
的縱坐標分別為m,n,求證:m與n的乘積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了比較兩種治療某病毒的藥(分別稱為甲藥,乙藥)的療效,某醫療團隊隨機地選取了服用甲藥的患者和服用乙藥的患者進行研究,根據研究的數據,繪制了如圖1等高條形圖
.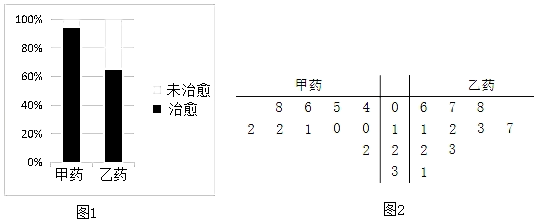
(1)根據等高條形圖,判斷哪一種藥的治愈率更高,不用說明理由;
(2)為了進一步研究兩種藥的療效,從服用甲藥的治愈患者和服用乙藥的治愈患者中,分別抽取了10名,記錄他們的治療時間(單位:天),統計并繪制了如圖2莖葉圖,從莖葉圖看,哪一種藥的療效更好,并說明理由;
(3)標準差s除了可以用來刻畫一組數據的離散程度外,還可以刻畫每個數據偏離平均水平的程度,如果出現了治療時間在(![]() 3s,
3s,![]() 3s)之外的患者,就認為病毒有可能發生了變異,需要對該患者進行進一步檢查,若某服用甲藥的患者已經治療了26天還未痊愈,請結合(2)中甲藥的數據,判斷是否應該對該患者進行進一步檢查?
3s)之外的患者,就認為病毒有可能發生了變異,需要對該患者進行進一步檢查,若某服用甲藥的患者已經治療了26天還未痊愈,請結合(2)中甲藥的數據,判斷是否應該對該患者進行進一步檢查?
參考公式:s![]() ,
,
參考數據:![]() 48.
48.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com