
【題目】已知函數(shù)f(x)=a(x﹣1)2+lnx+1,g(x)=f(x)﹣x,其中a∈R.
(Ⅰ)當a=﹣ ![]() 時,求函數(shù)f(x)的極值;
時,求函數(shù)f(x)的極值;
(Ⅱ)當a>0時,求函數(shù)g(x)的單調區(qū)間;
(Ⅲ)當x∈[1,+∞)時,若y=f(x)圖象上的點都在 ![]() 所表示的平面區(qū)域內,求實數(shù)a的取值范圍.
所表示的平面區(qū)域內,求實數(shù)a的取值范圍.
【答案】解:(Ⅰ)當a=﹣ ![]() 時,f(x)=﹣
時,f(x)=﹣ ![]() x2+
x2+ ![]() x+lnx+
x+lnx+ ![]() ,
,
f(x)的定義域為(0,+∞),f′(x)=﹣ ![]() ;
;
列表討論f′(x)和f(x)的變化情況:
x | (0,2) | 2 | (2,+∞) |
f′(x) | + | 0 | ﹣ |
f(x) | ↗ | 極大值 | ↘ |
∴當x=2時,f(x)取得極大值f(2)=ln2+ ![]() ;
;
(Ⅱ)當a>0時,g(x)=ax2﹣(2a+1)x+lnx+a+1,
g(x)的定義域為(0,+∞),
g′(x)= 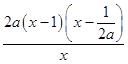 ,
,
令g′(x)=0,得x=1或x= ![]() ,
,
①當0<a< ![]() ,即
,即 ![]() >1時,
>1時,
由g′(x)<0,解得:1<x< ![]() ,
,
由g′(x)>0,解得:0<x<1或x> ![]() ,
,
∴g(x)在(1, ![]() )上單調遞減,
)上單調遞減,
在(0,1),( ![]() ,+∞)上單調遞增;
,+∞)上單調遞增;
②當a= ![]() ,即
,即 ![]() =1時,在(0,+∞)上,g′(x)≥0,
=1時,在(0,+∞)上,g′(x)≥0,
∴g(x)在(0,+∞)上單調遞增;
③當a> ![]() ,即0<
,即0< ![]() <1時,
<1時,
由g′(x)<0,解得 ![]() <x<1,由g′(x)>0,解得0<x<
<x<1,由g′(x)>0,解得0<x< ![]() 或x>1,
或x>1,
∴g(x)在( ![]() ,1)上單調遞減,
,1)上單調遞減,
在(0, ![]() ),(1,+∞)上單調遞增.
),(1,+∞)上單調遞增.
(Ⅲ)∵y=f(x)圖象上的點都在 ![]() 所表示的平面區(qū)域內,
所表示的平面區(qū)域內,
∴當x∈[1,+∞)時,f(x)﹣x≤0恒成立,
即當x∈[1,+∞)時,g(x)=a(x﹣1)2+lnx+1﹣x≤0恒成立.
只需g(x)max≤0;
①當a>0時,由(Ⅱ)知,
當0<a< ![]() 時,g(x)在(1,
時,g(x)在(1, ![]() )上單調遞減,在(
)上單調遞減,在( ![]() ,+∞)上單調遞增,
,+∞)上單調遞增,
∴g(x)在[1,+∞)上無最大值,不滿足條件;
當a≥ ![]() 時,g(x) 在(1,+∞)上單調遞增,
時,g(x) 在(1,+∞)上單調遞增,
∴g(x)在[1,+∞)上無最大值,不滿足條件;
②當a=0時,g′(x)=﹣ ![]() ,在(1,+∞)上,g′(x)<0,
,在(1,+∞)上,g′(x)<0,
∴g(x)在[1,+∞)上單調遞減,g(x)≤g(1)=0成立;
③當a<0時,g′(x)= 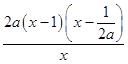 ,在(1,+∞)上,g′(x)<0,
,在(1,+∞)上,g′(x)<0,
∴g(x)在[1,+∞)上單調遞減,g(x)≤g(1)=0成立,
綜上可知,實數(shù)a的取值范圍是a≤0
【解析】(Ⅰ)求出函數(shù)的導數(shù),解關于導函數(shù)的不等式,求出函數(shù)的單調區(qū)間,從而求出函數(shù)的極大值即可;(Ⅱ)求出函數(shù)的導數(shù),通過討論a的范圍,求出函數(shù)的單調區(qū)間即可;(Ⅲ)問題轉化為x∈[1,+∞)時,g(x)=a(x﹣1)2+lnx+1﹣x≤0恒成立,只需g(x)max≤0即可,根據(jù)函數(shù)的單調性求出a的范圍.
【考點精析】利用利用導數(shù)研究函數(shù)的單調性和函數(shù)的極值與導數(shù)對題目進行判斷即可得到答案,需要熟知一般的,函數(shù)的單調性與其導數(shù)的正負有如下關系: 在某個區(qū)間![]() 內,(1)如果
內,(1)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調遞增;(2)如果
在這個區(qū)間單調遞增;(2)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調遞減;求函數(shù)
在這個區(qū)間單調遞減;求函數(shù)![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值.
是極小值.


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐S—ABCD的底面是正方形,側棱SA⊥底面ABCD,
過A作AE垂直SB交SB于E點,作AH垂直SD交SD于H點,平面AEH交SC于K點,且AB=1,SA=2.

(1)證明E、H在以AK為直徑的圓上,且當點P是SA上任一點時,試求![]() 的最小值;
的最小值;
(2)求平面AEKH與平面ABCD所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),圓
為參數(shù)),圓![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),圓
為參數(shù)),圓![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).若直線
為參數(shù)).若直線![]() 分別與圓
分別與圓![]() 和圓
和圓![]() 交于不同于原點的點
交于不同于原點的點![]() 和
和![]() .
.
(1)以直角坐標系的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,求圓
軸的正半軸為極軸,建立極坐標系,求圓![]() 和圓
和圓![]() 的極坐標方程;
的極坐標方程;
(2)求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,⊙O是以AB為直徑的圓,點C在圓上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延長線與AB的延長線交于點E.若EB=6,EC=6 ![]() ,則BC的長為 .
,則BC的長為 . 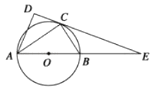
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】橢圓C: ![]() =1(a>b>0)的中心在原點,焦點在x軸上,焦距為2,且與橢圓x2+
=1(a>b>0)的中心在原點,焦點在x軸上,焦距為2,且與橢圓x2+ ![]() =1有相同離心率,直線l:y=kx+m與橢圓C交于不同的A,B兩點.
=1有相同離心率,直線l:y=kx+m與橢圓C交于不同的A,B兩點.
(Ⅰ)求橢圓C的方程;
(Ⅱ)若在橢圓C上存在點Q,滿足 ![]() ,(O為坐標原點),求實數(shù)λ取值范圍.
,(O為坐標原點),求實數(shù)λ取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在某測試中,卷面滿分為100分,60分為及格,為了調查午休對本次測試前兩個月復習效果的影響,特對復習中進行午休和不進行午休的考生進行了測試成績的統(tǒng)計,數(shù)據(jù)如下表所示:
分數(shù)段 | 29~ 40 | 41~ 50 | 51~ 60 | 61~ 70 | 71~ 80 | 81~ 90 | 91~ 100 |
午休考 生人數(shù) | 23 | 47 | 30 | 21 | 14 | 31 | 14 |
不午休 考生人數(shù) | 17 | 51 | 67 | 15 | 30 | 17 | 3 |
(1)根據(jù)上述表格完成列聯(lián)表:
及格人數(shù) | 不及格人數(shù) | 總計 | |
午休 | |||
不午休 | |||
總計 |
(2)根據(jù)列聯(lián)表可以得出什么樣的結論?對今后的復習有什么指導意義?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四面體ABCD中,AB、BC、BD兩兩垂直,AB=BC=BD=4,E、F分別為棱BC、AD的中點. 
(1)求異面直線AB與EF所成角的余弦值;
(2)求E到平面ACD的距離;
(3)求EF與平面ACD所成角的正弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com