
【題目】某學(xué)校微信公眾號(hào)收到非常多的精彩留言,學(xué)校從眾多留言者中抽取了100人參加“學(xué)校滿意度調(diào)查”,其留言者年齡集中在![]() 之間,根據(jù)統(tǒng)計(jì)結(jié)果,做出頻率分布直方圖如下:
之間,根據(jù)統(tǒng)計(jì)結(jié)果,做出頻率分布直方圖如下:

(1)求這100位留言者年齡的平均數(shù)和中位數(shù);
(2)學(xué)校從參加調(diào)查的年齡在![]() 和
和![]() 的留言者中,按照分層抽樣的方法,抽出了6人參加“精彩留言”經(jīng)驗(yàn)交流會(huì),贈(zèng)與年齡在
的留言者中,按照分層抽樣的方法,抽出了6人參加“精彩留言”經(jīng)驗(yàn)交流會(huì),贈(zèng)與年齡在![]() 的留言者每人一部價(jià)值1000元的手機(jī),年齡在
的留言者每人一部價(jià)值1000元的手機(jī),年齡在![]() 的留言者每人一套價(jià)值700元的書,現(xiàn)要從這6人中選出3人作為代表發(fā)言,求這3位發(fā)言者所得紀(jì)念品價(jià)值超過2300元的概率.
的留言者每人一套價(jià)值700元的書,現(xiàn)要從這6人中選出3人作為代表發(fā)言,求這3位發(fā)言者所得紀(jì)念品價(jià)值超過2300元的概率.
【答案】(1)60,![]() ;(2)
;(2)![]() .
.
【解析】
(1)直接利用頻率分布直方圖求得平均數(shù)和中位數(shù)即可;
(2)利用分層抽樣可得6人中年齡在![]() 內(nèi)有2人,設(shè)為
內(nèi)有2人,設(shè)為![]() 、
、![]() ,在
,在![]() 內(nèi)有4人,設(shè)為1,2,3,4,寫出基本事件,利用古典概型即可.
內(nèi)有4人,設(shè)為1,2,3,4,寫出基本事件,利用古典概型即可.
(1)這100位留言者年齡的樣本平均數(shù),
![]() ,
,
年齡在![]() 中的頻率為:
中的頻率為:![]() ,
,
年齡在![]() 中的頻率為:
中的頻率為:![]() ,
,
中位數(shù)在區(qū)間![]() 中,
中,
中位數(shù)為![]() .
.
(2)根據(jù)分層抽樣原理,可知這6人中年齡在![]() 內(nèi)有2人,設(shè)為
內(nèi)有2人,設(shè)為![]()
![]() ,
,
在![]() 內(nèi)有4人,設(shè)為1234.
內(nèi)有4人,設(shè)為1234.
設(shè)事件![]() 為“這3位發(fā)言者所得紀(jì)念品價(jià)值超過2300元”.
為“這3位發(fā)言者所得紀(jì)念品價(jià)值超過2300元”.
從這6人中選3人的所有基本事件有:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 123124134234,共20個(gè).
123124134234,共20個(gè).
其中事件![]() 的對(duì)立事件即3個(gè)人都是年齡
的對(duì)立事件即3個(gè)人都是年齡![]() 內(nèi),
內(nèi),
包含的有123124134234,共4個(gè).
(寫出事件![]() 的基本事件個(gè)數(shù)也可以)
的基本事件個(gè)數(shù)也可以)
所以![]() .,
.,


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖①,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=![]() AB=2.將△ADC沿AC折起,使平面ADC⊥平面ABC,得到幾何體DABC,如圖②所示.
AB=2.將△ADC沿AC折起,使平面ADC⊥平面ABC,得到幾何體DABC,如圖②所示.

(1)證明:平面ABD⊥平面BCD;
(2)求二面角DABC的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了了解某校學(xué)生喜歡吃零食是否與性別有關(guān),隨機(jī)對(duì)此校100人進(jìn)行調(diào)查,得到如下的列表:已知在全部100人中隨機(jī)抽取1人,抽到不喜歡吃零食的學(xué)生的概率為![]() .
.
喜歡吃零食 | 不喜歡吃零食辣 | 合計(jì) | |
男生 | 10 | ||
女生 | 20 | ||
合計(jì) | 100 |
(Ⅰ)請(qǐng)將上面的列表補(bǔ)充完整;
(Ⅱ)是否有99.9%以上的把握認(rèn)為喜歡吃零食與性別有關(guān)?說明理由.
下面的臨界值表供參考:![]() ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() ,其中
,其中![]() 為自然對(duì)數(shù)的底數(shù).
為自然對(duì)數(shù)的底數(shù).
(Ⅰ)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(Ⅱ)若對(duì)任意![]() ,不等式
,不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)試探究當(dāng)![]() 時(shí),方程
時(shí),方程![]() 的解的個(gè)數(shù),并說明理由.
的解的個(gè)數(shù),并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)=|2x-1|-|x+1|.
(1)將f(x)的解析式寫成分段函數(shù)的形式,并作出其圖象;
(2)若a+b=1,對(duì)a,b∈(0,+∞),![]() +
+![]() ≥3f(x)恒成立,求x的取值范圍.
≥3f(x)恒成立,求x的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某火鍋店為了了解氣溫對(duì)營業(yè)額的影響,隨機(jī)記錄了該店1月份其中5天的日營業(yè)額y(單位:萬元)與該地當(dāng)日最低氣溫x(單位:℃)的數(shù)據(jù),如下表:
![]()
(1)求y關(guān)于x的線性回歸方程![]() =
=![]() x+
x+![]() ;
;
(2)判斷y與x之間是正相關(guān)還是負(fù)相關(guān),若該地1月份某天的最低氣溫為6 ℃,用所求回歸方程預(yù)測(cè)該店當(dāng)日的營業(yè)額;
(3)設(shè)該地1月份的日最低氣溫X~N(μ,σ2),其中μ近似為樣本平均數(shù)![]() ,σ2近似為樣本方差s2,求P(3.8<X≤13.4).
,σ2近似為樣本方差s2,求P(3.8<X≤13.4).
附:①回歸方程![]() 中,
中,![]() =
=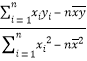 ,
,![]() =
=![]() ﹣
﹣![]() .
.
②![]() ≈3.2,
≈3.2,![]() ≈1.8.若X~N(μ,σ2),則P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
≈1.8.若X~N(μ,σ2),則P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,橢圓
中,橢圓![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,離心率為
,離心率為![]() . 已知過點(diǎn)
. 已知過點(diǎn)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn).
兩點(diǎn).

(1)求橢圓![]() 的方程;
的方程;
(2)試問![]() 軸上是否存在定點(diǎn)
軸上是否存在定點(diǎn)![]() ,使得
,使得![]() 為定值.若存在,求出點(diǎn)
為定值.若存在,求出點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說明理由.
的坐標(biāo);若不存在,請(qǐng)說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com