Question

【題目】我校舉行的 “青年歌手大選賽”吸引了眾多有才華的學生參賽．為了了解本次比賽成績情況，從中抽取了50名學生的成績（得分取正整數，滿分為100分）作為樣本進行統計．請根據下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖（如圖所示）解決下列問題：

組別	分組	頻數	頻率
第1組	[50，60）	8	0.16
第2組	[60，70）	a	▓
第3組	[70，80）	20	0.40
第4組	[80，90）	▓	0.08
第5組	[90，100]	2	b
	合計	▓	▓

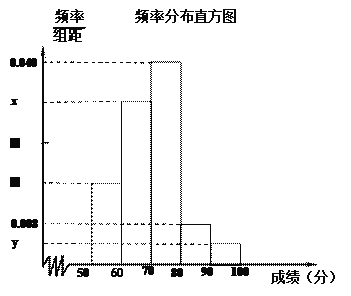
（1）求出的值；

（2）在選取的樣本中，從成績是80分以上（含80分）的同學中隨機抽取2名同學參加元旦晚會，求所抽取的2名同學中至少有1名同學來自第5組的概率；

（3）根據頻率分布直方圖，估計這50名學生成績的眾數、中位數和平均數。

Answer 1

【答案】（1）16，0.04，0.032，0.004；（2）；（3）

【解析】試題分析：（1）根據頻率分布表及頻率分布圖即可求出；（2）列舉所有基本事件，找出所抽取的2名同學中至少有1名同學來自第5組的基本事件，即可利用古典概型計算；（3）根據頻率分布直方圖計算眾數、中位數、平均數。

試題解析：（1）由題意可知，．

（2）由題意可知，第4組共有4人，記為 ，第5組共有2人，記為．

從競賽成績是80分以上（含80分）的同學中隨機抽取2名同學有，，共15種情況．

設“隨機抽取的2名同學中至少有1名同學來自第5組”為事件E，

有共9種情況．

所以隨機抽取的2名同學中至少有1名同學來自第5組的概率是．

（3）眾數75，中位數70．5，

平均數