
【題目】設(shè)△ABC三個內(nèi)角A、B、C所對的邊分別為![]() 已知
已知![]()
(1)求角B的大小;
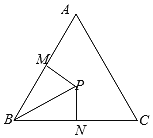
(2)如圖,在△ABC內(nèi)取一點P,使得PB=2,過點P分別作直線BA、BC的垂線PM、PN,垂足分別是M、N,設(shè)∠PBA=![]() 求四邊形PMBN的面積的最大值及此時
求四邊形PMBN的面積的最大值及此時![]() 的值.
的值.
【答案】(1)B![]() (2)α
(2)α![]() 時,四邊形PMBN的面積取得最大值
時,四邊形PMBN的面積取得最大值![]() .
.
【解析】
(1)由acosA=bcosB及正弦定理可得:sinAcosA=sinBcosB,即sin2A=sin2B,又A∈(0,π),B∈(0,π),可得A=B或A+B![]() . 由于C
. 由于C![]() ,即可得出.
,即可得出.
(2)由題設(shè),在Rt△PMB中,PM=2sinα;PN=2cosα,得其面積;在Rt△PNB中,同理可得PN=2sin(![]() α),PM=2cos(
α),PM=2cos(![]() α),α∈(0,
α),α∈(0,![]() )得其面積,進而得四邊形面積,利用恒等變換結(jié)合三角函數(shù)最值即可得出.
)得其面積,進而得四邊形面積,利用恒等變換結(jié)合三角函數(shù)最值即可得出.
(1)由acosA=bcosB及正弦定理可得:sinAcosA=sinBcosB,
即sin2A=sin2B,又A∈(0,π),B∈(0,π),
∴有A=B或A+B![]() .
.
又∵C![]() ,得A+B
,得A+B![]() ,與A+B
,與A+B![]() 矛盾,
矛盾,
∴A=B,因此B![]() .
.
(2)由題設(shè),得在Rt△PMB中,PM=PBsin∠PBM=2sinα;PN=PBcos∠PBM=2cosα,則![]()
同理,在Rt△PNB中,PN=PBsin∠PBN=PBsin(![]() ∠PBA)=2sin(
∠PBA)=2sin(![]() α),PM=2cos(
α),PM=2cos(![]() α)α∈(0,
α)α∈(0,![]() ),
),![]()
∴四邊形PMBN的面積![]()
∵α∈(0,![]() ),∴2α
),∴2α![]() ∈(
∈(![]() ,
,![]() ),
),
于是,當(dāng)2α![]() ,即α
,即α![]() 時,四邊形PMBN的面積取得最大值
時,四邊形PMBN的面積取得最大值![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】世界那么大,我想去看看,處在具有時尚文化代表的大學(xué)生們旅游動機強烈,旅游可支配收入日益增多,可見大學(xué)生旅游是一個巨大的市場.為了解大學(xué)生每年旅游消費支出(單位:百元)的情況,相關(guān)部門隨機抽取了某大學(xué)的![]() 名學(xué)生進行問卷調(diào)查,并把所得數(shù)據(jù)列成如下所示的頻數(shù)分布表:
名學(xué)生進行問卷調(diào)查,并把所得數(shù)據(jù)列成如下所示的頻數(shù)分布表:
組別 |
|
|
|
|
|
頻數(shù) |
|
|
|
|
|
(Ⅰ)求所得樣本的中位數(shù)(精確到百元);
(Ⅱ)根據(jù)樣本數(shù)據(jù),可近似地認(rèn)為學(xué)生的旅游費用支出![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,若該所大學(xué)共有學(xué)生
,若該所大學(xué)共有學(xué)生![]() 人,試估計有多少位同學(xué)旅游費用支出在
人,試估計有多少位同學(xué)旅游費用支出在![]() 元以上;
元以上;
(Ⅲ)已知樣本數(shù)據(jù)中旅游費用支出在![]() 范圍內(nèi)的
范圍內(nèi)的![]() 名學(xué)生中有
名學(xué)生中有![]() 名女生,
名女生, ![]() 名男生,現(xiàn)想選其中
名男生,現(xiàn)想選其中![]() 名學(xué)生回訪,記選出的男生人數(shù)為
名學(xué)生回訪,記選出的男生人數(shù)為![]() ,求
,求![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
附:若![]() ,則
,則![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為圓
為圓![]() 上一動點,圓心
上一動點,圓心![]() 關(guān)于
關(guān)于![]() 軸的對稱點為
軸的對稱點為![]() ,點
,點![]() 分別是線段
分別是線段![]() 上的點,且
上的點,且![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)直線![]() 與點
與點![]() 的軌跡
的軌跡![]() 只有一個公共點
只有一個公共點![]() ,且點
,且點![]() 在第二象限,過坐標(biāo)原點
在第二象限,過坐標(biāo)原點![]() 且與
且與![]() 垂直的直線
垂直的直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓![]() 的離心率是
的離心率是![]() ,過點
,過點![]() 的動直線
的動直線![]() 與橢圓相交于
與橢圓相交于![]() 兩點,當(dāng)直線
兩點,當(dāng)直線![]() 與
與![]() 軸平行時,直線
軸平行時,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)在![]() 軸上是否存在異于點
軸上是否存在異于點![]() 的定點
的定點![]() ,使得直線
,使得直線![]() 變化時,總有
變化時,總有![]() ?若存在,求出點
?若存在,求出點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列![]() 滿足
滿足![]() ,其中
,其中![]() ,且
,且![]() 為常數(shù).
為常數(shù).
(1)若![]() 是等差數(shù)列,且公差
是等差數(shù)列,且公差![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且數(shù)列
,且數(shù)列![]() 滿足
滿足![]() 對任意的
對任意的![]() 都成立.
都成立.
①求數(shù)列![]() 的前
的前![]() 項之和
項之和![]() ;
;
②若![]() 對任意的
對任意的![]() 都成立,求
都成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)二次函數(shù)![]() 的圖像過點
的圖像過點![]() 和
和![]() ,且對于任意實數(shù)
,且對于任意實數(shù)![]() ,不等式
,不等式![]() 恒成立
恒成立
(1)求![]() 的表達式;
的表達式;
(2)設(shè)![]() ,若
,若![]() 在
在![]() 上是增函數(shù),求實數(shù)
上是增函數(shù),求實數(shù)![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的左焦點為
)的左焦點為![]() ,左準(zhǔn)線方程為
,左準(zhǔn)線方程為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)已知直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點.
兩點.
①若直線![]() 經(jīng)過橢圓
經(jīng)過橢圓![]() 的左焦點
的左焦點![]() ,交
,交![]() 軸于點
軸于點![]() ,且滿足
,且滿足![]() ,
, ![]() .求證:
.求證: ![]() 為定值;
為定值;
②若![]() (
(![]() 為原點),求
為原點),求![]() 面積的取值范圍.
面積的取值范圍.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=Asin(ωx![]() )+1(A>0,ω>0)的最大值為3,其圖象相鄰兩條對稱軸之間的距離為
)+1(A>0,ω>0)的最大值為3,其圖象相鄰兩條對稱軸之間的距離為![]() .
.
(1)求函數(shù)f(x)的解析式;
(2)求函數(shù)y=f(x)的單調(diào)增區(qū)間;
(3)設(shè)α∈(0,![]() ),則f(
),則f(![]() )=2,求α的值.
)=2,求α的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】水培植物需要一種植物專用營養(yǎng)液,已知每投放![]() 且
且![]() 個單位的營養(yǎng)液,它在水中釋放的濃度
個單位的營養(yǎng)液,它在水中釋放的濃度![]() (克/升)隨著時間
(克/升)隨著時間![]() (天)變化的函數(shù)關(guān)系式近似為
(天)變化的函數(shù)關(guān)系式近似為![]() ,其中
,其中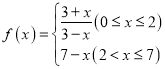 ,若多次投放,則某一時刻水中的營養(yǎng)液濃度為每次投放的營養(yǎng)液在相應(yīng)時刻所釋放的濃度之和,根據(jù)經(jīng)驗,當(dāng)水中營養(yǎng)液的濃度不低于4(克/升)時,它才能有效.
,若多次投放,則某一時刻水中的營養(yǎng)液濃度為每次投放的營養(yǎng)液在相應(yīng)時刻所釋放的濃度之和,根據(jù)經(jīng)驗,當(dāng)水中營養(yǎng)液的濃度不低于4(克/升)時,它才能有效.
(1)若只投放一次2個單位的營養(yǎng)液,則有效時間最多可能持續(xù)幾天?
(2)若先投放2個單位的營養(yǎng)液,4天后再投放b個單位的營養(yǎng)液,要使接下來的2天中,營養(yǎng)液能夠持續(xù)有效,試求![]() 的最小值.
的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com