
【題目】在平面直角坐標系![]() 中,已知拋物線
中,已知拋物線![]() 上的點
上的點![]() 到焦點
到焦點![]() 的距離為2.
的距離為2.
(1)求拋物線的方程;
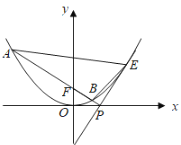
(2)如圖,點![]() 是拋物線上異于原點的點,拋物線在點
是拋物線上異于原點的點,拋物線在點![]() 處的切線與
處的切線與![]() 軸相交于點
軸相交于點![]() ,直線
,直線![]() 與拋物線相交于
與拋物線相交于![]() 兩點,求
兩點,求![]() 面積的最小值.
面積的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出拋物線![]() 的準線方程為
的準線方程為![]() ,由拋物線定義,得到
,由拋物線定義,得到![]() ,即可求解拋物線的方程.
,即可求解拋物線的方程.
(2)求出函數的![]() .設點
.設點![]() ,得到拋物線在點
,得到拋物線在點![]() 處的切線方程為
處的切線方程為![]() .求出
.求出![]() .推出直線
.推出直線![]() 的方程,點
的方程,點![]() 到直線
到直線![]() 的距離,聯立
的距離,聯立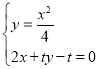 求出
求出![]() ,表示出
,表示出![]() 的面積,構造函數,通過函數的導數利用單調性求解最值即可.
的面積,構造函數,通過函數的導數利用單調性求解最值即可.
(1)拋物線![]() 的準線方程為
的準線方程為![]() ,
,
因為![]() ,由拋物線定義,知
,由拋物線定義,知![]() ,
,
所以![]() ,即
,即![]() ,
,
所以拋物線的方程為![]() .
.
(2)因為![]() ,所以
,所以![]() .
.
設點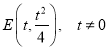 ,則拋物線在點
,則拋物線在點![]() 處的切線方程為
處的切線方程為![]() .
.
令![]() ,則
,則![]() ,即點
,即點![]() .
.
因為![]() 所以直線PF的方程為
所以直線PF的方程為![]() ,即
,即![]() .
.
則點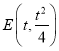 到直線
到直線![]() 的距離為
的距離為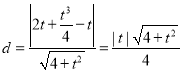 .
.
聯立方程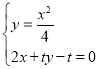 消元,得
消元,得![]() .
.
因為![]() ,
,
所以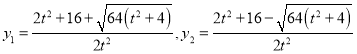 ,
,
所以![]() .
.
所以![]() 的面積為
的面積為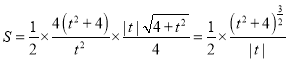 .
.
不妨設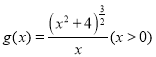 ,則
,則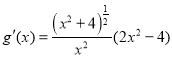 .
.
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 上,
上,![]() ,所以
,所以![]() 在
在![]() 上單調遞增,
上單調遞增,
所以當![]() 時,
時,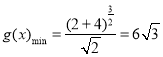 .
.
所以![]() 的面積的最小值為
的面積的最小值為![]() .
.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如下圖,在四棱錐![]() 中,
中,![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點。
的中點。
(1)求證:![]() 面
面![]() ;
;
(2)線段![]() 上是否存在一點
上是否存在一點![]() ,滿足
,滿足![]() ?若存在,試求出二面角
?若存在,試求出二面角![]() 的余弦值;若不存在,說明理由。
的余弦值;若不存在,說明理由。

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某創新團隊擬開發一種新產品,根據市場調查估計能獲得10萬元到1000萬元的收益,先準備制定一個獎勵方案:獎金![]() (單位:萬元)隨收益
(單位:萬元)隨收益![]() (單位:萬元)的增加而增加,且獎金不超過9萬元,同時獎金不超過收益的20%.
(單位:萬元)的增加而增加,且獎金不超過9萬元,同時獎金不超過收益的20%.
(1)若建立函數![]() 模型制定獎勵方案,試用數學語言表示該團隊對獎勵函數
模型制定獎勵方案,試用數學語言表示該團隊對獎勵函數![]() 模型的基本要求,并分析
模型的基本要求,并分析![]() 是否符合團隊要求的獎勵函數模型,并說明原因;
是否符合團隊要求的獎勵函數模型,并說明原因;
(2)若該團隊采用模型函數![]() 作為獎勵函數模型,試確定最小的正整數
作為獎勵函數模型,試確定最小的正整數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 參數方程為
參數方程為![]() 為參數),將曲線
為參數),將曲線![]() 上所有點的橫坐標變為原來的
上所有點的橫坐標變為原來的![]() ,縱坐標變為原來的
,縱坐標變為原來的![]() ,得到曲線
,得到曲線![]() .
.
(1)求曲線![]() 的普通方程;
的普通方程;
(2)過點![]() 且傾斜角為
且傾斜角為![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 取得最小值時
取得最小值時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,一個長軸頂點在直線
,一個長軸頂點在直線![]() 上,若直線
上,若直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,
兩點,![]() 為坐標原點,直線
為坐標原點,直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() .
.
(1)求該橢圓的方程.
(2)若![]() ,試問
,試問![]() 的面積是否為定值?若是,求出這個定值;若不是,請說明理由.
的面積是否為定值?若是,求出這個定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】紙張的規格是指紙張制成后,經過修整切邊,裁成一定的尺寸.現在我國采用國際標準,規定以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 等標記來表示紙張的幅面規格.復印紙幅面規格只采用
等標記來表示紙張的幅面規格.復印紙幅面規格只采用![]() 系列和
系列和![]() 系列,其中系列的幅面規格為:①
系列,其中系列的幅面規格為:①![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 所有規格的紙張的幅寬(以
所有規格的紙張的幅寬(以![]() 表示)和長度(以
表示)和長度(以![]() 表示)的比例關系都為
表示)的比例關系都為![]() ;②將
;②將![]() 紙張沿長度方向對開成兩等分,便成為
紙張沿長度方向對開成兩等分,便成為![]() 規格,
規格,![]() 紙張沿長度方向對開成兩等分,便成為
紙張沿長度方向對開成兩等分,便成為![]() 規格,…,如此對開至
規格,…,如此對開至![]() 規格.現有
規格.現有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 紙各一張.若
紙各一張.若![]() 紙的寬度為
紙的寬度為![]() ,則
,則![]() 紙的面積為________
紙的面積為________![]() ;這
;這![]() 張紙的面積之和等于________
張紙的面積之和等于________![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知函數![]() .(
.(![]() 是常數,且(
是常數,且(![]() )
)
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)當![]() 在
在![]() 處取得極值時,若關于
處取得極值時,若關于![]() 的方程
的方程![]() 在
在![]() 上恰有兩個不相等的實數根,求實數
上恰有兩個不相等的實數根,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)求證:當![]() 時
時![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2021年我省將實施新高考,新高考“依據統一高考成績、高中學業水平考試成績,參考高中學生綜合素質評價信息”進行人才選拔。我校2018級高一年級一個學習興趣小組進行社會實踐活動,決定對某商場銷售的商品A進行市場銷售量調研,通過對該商品一個階段的調研得知,發現該商品每日的銷售量![]() (單位:百件)與銷售價格
(單位:百件)與銷售價格![]() (元/件)近似滿足關系式
(元/件)近似滿足關系式![]() ,其中
,其中![]() 為常數
為常數![]() 已知銷售價格為3元/件時,每日可售出該商品10百件。
已知銷售價格為3元/件時,每日可售出該商品10百件。
(1)求函數![]() 的解析式;
的解析式;
(2)若該商品A的成本為2元/件,根據調研結果請你試確定該商品銷售價格的值,使該商場每日銷售該商品所獲得的利潤(單位:百元)最大。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com