
【題目】已知四個函數![]() ,其中
,其中![]() ,
,![]() 的圖像如圖所示.
的圖像如圖所示.

(1)請在坐標系中畫出![]() ,
,![]() 的圖像,并根據這四個函數的圖像總結出指數函數具有哪些性質?
的圖像,并根據這四個函數的圖像總結出指數函數具有哪些性質?
(2)舉出在實際情境中能夠抽象出指數函數的一個例子并說明理由.
【答案】(1)圖象見解析,性質見解析;(2)舉例及理由見解析
【解析】
(1)列表,描點,連線可得圖象; 利用圖象向左右變化趨勢可得定義域,上下變化趨勢可得值域,從左向右看上升和下降可得單調性.
(2) 舉細胞分裂的例子.
(1)畫出![]() ,
,![]() 的圖像如圖所示.
的圖像如圖所示.
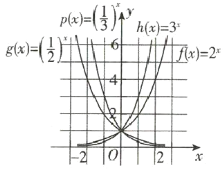
4個函數都是![]() (
(![]() 且
且![]() )的形式,它們的性質包括:
)的形式,它們的性質包括:
①定義域為R.
②值域為![]() .
.
③都過定點![]() .
.
④當![]() 時,函數在定義域內單調遞增;
時,函數在定義域內單調遞增;
當![]() 時,函數在定義域內單調遞減.
時,函數在定義域內單調遞減.
⑤當![]() 時,若
時,若![]() ,則
,則 ![]() ,若
,若![]() ,則
,則 ![]() ;
;
當![]() 時,若
時,若 ![]() ,則
,則 ![]() ,若
,若![]() ,則
,則![]() .
.
⑥對于函數 ![]() (
(![]() 且
且![]() ),
),![]() (
(![]() 且
且![]() ),當
),當 ![]() 時,若
時,若![]() ,則
,則
![]() ;若
;若![]() ,則
,則 ![]() ;若
;若 ![]() ,則
,則 ![]() .
.
當![]() 時,若
時,若![]() ,則
,則 ![]() ;若
;若![]() ,則
,則 ![]() ;若
;若 ![]() ,則
,則
![]() .
.
(2)舉例:細胞分裂的規(guī)則是細胞由一個分裂成2個,這兩個細胞分裂成2個…若原來有1個細胞,經過x次分裂,細胞個數為y,則![]() 是一個指數函數.
是一個指數函數.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C:![]() 與直線l:
與直線l:![]() 交于M,N兩點.
交于M,N兩點.
![]() 當
當![]() 時,求
時,求![]() 的面積的取值范圍;
的面積的取值范圍;
![]() 軸上是否存在點P,使得當k變動時,總有
軸上是否存在點P,使得當k變動時,總有![]() ?若存在,求以線段OP為直徑的圓的方程;若不存在,請說明理由.
?若存在,求以線段OP為直徑的圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形,E、F分別為PC、BD的中點,側面PAD⊥底面ABCD.
(1)求證:EF∥平面PAD;
(2)若EF⊥PC,求證:平面PAB⊥平面PCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于區(qū)間[a,b](a<b),若函數![]() 同時滿足:①
同時滿足:①![]() 在[a,b]上是單調函數,②函數
在[a,b]上是單調函數,②函數![]() 在[a,b]的值域是[a,b],則稱區(qū)間[a,b]為函數
在[a,b]的值域是[a,b],則稱區(qū)間[a,b]為函數![]() 的“保值”區(qū)間
的“保值”區(qū)間
(1)求函數![]() 的所有“保值”區(qū)間
的所有“保值”區(qū)間
(2)函數![]() 是否存在“保值”區(qū)間?若存在,求
是否存在“保值”區(qū)間?若存在,求![]() 的取值范圍,若不存在,說明理由
的取值范圍,若不存在,說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,點P
,點P![]() 在C上.
在C上.
(1)求橢圓C的方程;
(2)設![]() 分別為橢圓C的左右焦點,過
分別為橢圓C的左右焦點,過![]() 的直線
的直線![]() 與橢圓C交于不同的兩點A、B,求△
與橢圓C交于不同的兩點A、B,求△![]() 的內切圓的半徑的最大值.
的內切圓的半徑的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有4張牌(如圖)每張牌的一面都寫上一個英文字母,另一面都寫上一個數字.規(guī)定:當牌的一面為字母![]() 時,它的另一面必須寫數字2.你的任務是:為了檢驗下面的4張牌是否有違反規(guī)定的寫法,你翻看哪幾張牌就夠了.你的選擇是( ).
時,它的另一面必須寫數字2.你的任務是:為了檢驗下面的4張牌是否有違反規(guī)定的寫法,你翻看哪幾張牌就夠了.你的選擇是( ).
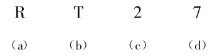
A. ![]() B.
B. ![]() 、
、![]()
C. ![]() 、
、![]() D. 非以上答案
D. 非以上答案
查看答案和解析>>
科目:高中數學 來源: 題型:
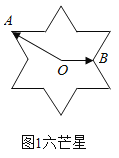
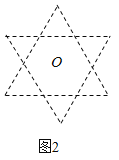
【題目】如圖,“六芒星”是由兩個全等正三角形組成,中心重合于點![]() 且三組對邊分別平行,點
且三組對邊分別平行,點![]() 是“六芒星”(如圖)的兩個頂點,動點
是“六芒星”(如圖)的兩個頂點,動點![]() 在“六芒星”上(內部以及邊界),若
在“六芒星”上(內部以及邊界),若![]() ,則
,則![]() 的取值可能是( )
的取值可能是( )
A.![]() B.1C.5D.9
B.1C.5D.9
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com