
已知函數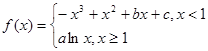
 的圖象過坐標原點O,且在點
的圖象過坐標原點O,且在點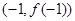 處的切線的斜率是
處的切線的斜率是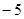 .
.
(1)求實數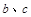 的值;
的值;
(2)求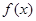 在區間
在區間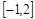 上的最大值;
上的最大值;
(3)對任意給定的正實數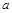 ,曲線
,曲線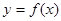 上是否存在兩點P、Q,使得
上是否存在兩點P、Q,使得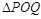 是以O為直角頂點的直角三角形,且此三角形斜邊中點在
是以O為直角頂點的直角三角形,且此三角形斜邊中點在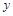 軸上?說明理由.
軸上?說明理由.
(1)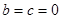 ;( Ⅱ)詳見解析;( Ⅲ)詳見解析.
;( Ⅱ)詳見解析;( Ⅲ)詳見解析.
解析試題分析:(1)當x<1時,f(x)=-x3+x2+bx+c,則f'(x)=-3x2+2x+b.依題意得: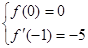 ,由此能求出實數b,c的值.(2)由
,由此能求出實數b,c的值.(2)由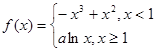 知,當-1≤x<1時,
知,當-1≤x<1時,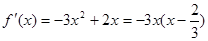 ,令f'(x)=0得
,令f'(x)=0得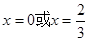 ,當x變化時,f'(x),f(x)的變化情況列表知f(x)在[-1,1)上的最大值為2.當1≤x≤2時,f(x)=alnx.當a≤0時,f(x)≤0,f(x)最大值為0;當a>0時,f(x)在[1,2]上單調遞增.當aln2≤2時,f(x)在區間[-1,2]上的最大值為2;當aln2>2時,f(x)在區間[-1,2]上的最大值為aln2.(3)假設曲線y=f(x)上存在兩點P、Q滿足題設要求,則點P、Q只能在y軸兩側.設P(t,f(t))(t>0),則Q(-t,t3+t2),顯然t≠1.由此入手能得到對任意給定的正實數a,曲線y=f(x)上存在兩點P、Q,使得△POQ是以O為直角頂點的直角三角形,且此三角形斜邊中點在y軸上.
,當x變化時,f'(x),f(x)的變化情況列表知f(x)在[-1,1)上的最大值為2.當1≤x≤2時,f(x)=alnx.當a≤0時,f(x)≤0,f(x)最大值為0;當a>0時,f(x)在[1,2]上單調遞增.當aln2≤2時,f(x)在區間[-1,2]上的最大值為2;當aln2>2時,f(x)在區間[-1,2]上的最大值為aln2.(3)假設曲線y=f(x)上存在兩點P、Q滿足題設要求,則點P、Q只能在y軸兩側.設P(t,f(t))(t>0),則Q(-t,t3+t2),顯然t≠1.由此入手能得到對任意給定的正實數a,曲線y=f(x)上存在兩點P、Q,使得△POQ是以O為直角頂點的直角三角形,且此三角形斜邊中點在y軸上.
解:(1)當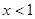 時,
時,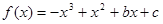 ,則
,則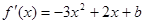 。
。
依題意得: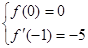 ,即
,即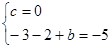 解得
解得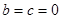
(2)由(1)知,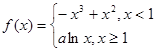
①當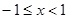 時,
時,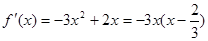 ,
,
令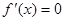 得
得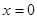 或
或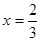
當 變化時,
變化時,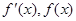 的變化情況如下表:
的變化情況如下表: