
【題目】直線l:ax+![]() y﹣1=0與x,y軸的交點分別為A,B,直線l與圓O:x2+y2=1的交點為C,D,給出下面三個結論:①a≥1,S△AOB=
y﹣1=0與x,y軸的交點分別為A,B,直線l與圓O:x2+y2=1的交點為C,D,給出下面三個結論:①a≥1,S△AOB=![]() ;②a≥1,|AB|<|CD|;③a≥1,S△COD<
;②a≥1,|AB|<|CD|;③a≥1,S△COD<![]() .其中,所有正確結論的序號是( )
.其中,所有正確結論的序號是( )
A.①②B.②③C.①③D.①②③
【答案】C
【解析】
①當a≥1時,分別可得直線的截距,由三角形的面積公式易得結論①正確;②當a≥1時,反證法可得結論②錯誤;③由三角形的面積公式可得S△COD![]() sin∠AOC
sin∠AOC![]() ,可得結論③正確.
,可得結論③正確.
解:①當a≥1時,把x=0代入直線方程可得y=a,把y=0代入直線方程可得x![]() ,
,
∴S△AOB![]() a
a![]() ,故結論①正確;
,故結論①正確;
②當a≥1時,|AB|![]() ,故|AB|2=a2
,故|AB|2=a2![]() ,
,
直線l可化為a2x+y﹣a=0,圓心O到l的距離d![]()
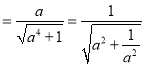 ,故|CD|2=4(1﹣d2)=4(1
,故|CD|2=4(1﹣d2)=4(1 ),
),
假設|AB|<|CD|,則|AB|2<|CD|2,即a2![]() 4(1
4(1 ),
),
整理可得(a2![]() )2﹣4(a2
)2﹣4(a2![]() )+4<0,即(a2
)+4<0,即(a2![]() 2)2<0,
2)2<0,
顯然矛盾,故結論②錯誤;
S△COD![]() |OA||OC|sin∠AOC
|OA||OC|sin∠AOC![]() sin∠AOC
sin∠AOC![]() ,
,
故a≥1,使得S△COD![]() ,結論③正確.
,結論③正確.
故選:C.


科目:高中數學 來源: 題型:
【題目】已知![]() 的圖像關于坐標原點對稱.
的圖像關于坐標原點對稱.
(1)求![]() 的值;
的值;
(2)若函數![]() 在
在![]() 內存在零點,求實數
內存在零點,求實數![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求滿足條件的最小整數
上恒成立,求滿足條件的最小整數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某款冰淇淋的包裝盒為圓臺,盒蓋為直徑為![]() 的圓形紙片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一個,假定每個冰淇淋球都是半徑為
的圓形紙片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一個,假定每個冰淇淋球都是半徑為![]() 的球體,三個冰淇淋球兩兩相切,且都與冰淇淋盒蓋、盒底和盒子側面的曲面相切,則冰淇淋盒的體積為______.
的球體,三個冰淇淋球兩兩相切,且都與冰淇淋盒蓋、盒底和盒子側面的曲面相切,則冰淇淋盒的體積為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
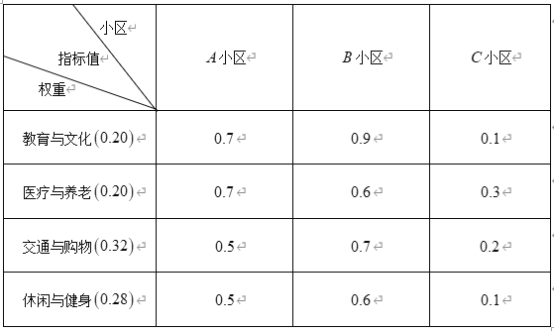
【題目】某市《城市總體規劃(![]() 年)》提出到
年)》提出到![]() 年實現“
年實現“![]() 分鐘社區生活圈”全覆蓋的目標,從教育與文化、醫療與養老、交通與購物、休閑與健身
分鐘社區生活圈”全覆蓋的目標,從教育與文化、醫療與養老、交通與購物、休閑與健身![]() 個方面構建“
個方面構建“![]() 分鐘社區生活圈”指標體系,并依據“
分鐘社區生活圈”指標體系,并依據“![]() 分鐘社區生活圈”指數高低將小區劃分為:優質小區(指數為
分鐘社區生活圈”指數高低將小區劃分為:優質小區(指數為![]() )、良好小區(指數為
)、良好小區(指數為![]() )、中等小區(指數為
)、中等小區(指數為![]() )以及待改進小區(指數為
)以及待改進小區(指數為![]() )
)![]() 個等級.下面是三個小區
個等級.下面是三個小區![]() 個方面指標的調查數據:
個方面指標的調查數據:
注:每個小區“![]() 分鐘社區生活圈”指數
分鐘社區生活圈”指數![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 為該小區四個方面的權重,
為該小區四個方面的權重,![]() 、
、![]() 、
、![]() 、
、![]() 為該小區四個方面的指標值(小區每一個方面的指標值為
為該小區四個方面的指標值(小區每一個方面的指標值為![]() 之間的一個數值).
之間的一個數值).
現有![]() 個小區的“
個小區的“![]() 分鐘社區生活圈”指數數據,整理得到如下頻數分布表:
分鐘社區生活圈”指數數據,整理得到如下頻數分布表:
分組 |
|
|
|
|
|
頻數 |
|
|
|
|
|
(Ⅰ)分別判斷![]() 、
、![]() 、
、![]() 三個小區是否是優質小區,并說明理由;
三個小區是否是優質小區,并說明理由;
(Ⅱ)對這![]() 個小區按照優質小區、良好小區、中等小區和待改進小區進行分層抽樣,抽取
個小區按照優質小區、良好小區、中等小區和待改進小區進行分層抽樣,抽取![]() 個小區進行調查,若在抽取的
個小區進行調查,若在抽取的![]() 個小區中再隨機地選取
個小區中再隨機地選取![]() 個小區做深入調查,記這
個小區做深入調查,記這![]() 個小區中為優質小區的個數
個小區中為優質小區的個數![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題P:函數![]() 且|f(a)|<2,命題Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
且|f(a)|<2,命題Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
(1)分別求命題P、Q為真命題時的實數a的取值范圍;
(2)當實數a取何范圍時,命題P、Q中有且僅有一個為真命題;
(3)設P、Q皆為真時a的取值范圍為集合S,![]() ,若RTS,求m的取值范圍.
,若RTS,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,沿河有A、B兩城鎮,它們相距![]() 千米.以前,兩城鎮的污水直接排入河里,現為保護環境,污水需經處理才能排放.兩城鎮可以單獨建污水處理廠,或者聯合建污水處理廠(在兩城鎮之間或其中一城鎮建廠,用管道將污水從各城鎮向污水處理廠輸送).依據經驗公式,建廠的費用為
千米.以前,兩城鎮的污水直接排入河里,現為保護環境,污水需經處理才能排放.兩城鎮可以單獨建污水處理廠,或者聯合建污水處理廠(在兩城鎮之間或其中一城鎮建廠,用管道將污水從各城鎮向污水處理廠輸送).依據經驗公式,建廠的費用為![]() (萬元),
(萬元),![]() 表示污水流量;鋪設管道的費用(包括管道費)
表示污水流量;鋪設管道的費用(包括管道費)![]() (萬元),
(萬元),![]() 表示輸送污水管道的長度(千米).已知城鎮A和城鎮B的污水流量分別為
表示輸送污水管道的長度(千米).已知城鎮A和城鎮B的污水流量分別為![]() 、
、![]() ,
,![]() 、
、![]() 兩城鎮連接污水處理廠的管道總長為
兩城鎮連接污水處理廠的管道總長為![]() 千米.假定:經管道輸送的污水流量不發生改變,污水經處理后直接排入河中.請解答下列問題(結果精確到
千米.假定:經管道輸送的污水流量不發生改變,污水經處理后直接排入河中.請解答下列問題(結果精確到![]() ):
):
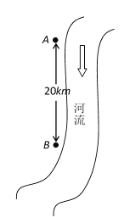
(1)若在城鎮A和城鎮B單獨建廠,共需多少總費用?
(2)考慮聯合建廠可能節約總投資,設城鎮A到擬建廠的距離為![]() 千米,求聯合建廠的總費用
千米,求聯合建廠的總費用![]() 與
與![]() 的函數關系式,并求
的函數關系式,并求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD是平行四邊形,且AB=1,BC=2, ∠ABC=60°,PA⊥平面ABCD,AE⊥PC于E,
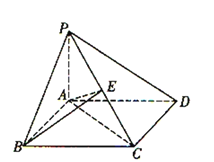
下列四個結論:①AB⊥AC;②AB⊥平面PAC;③PC⊥平面ABE;④BE⊥PC.正確的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com