
【題目】如圖甲,在直角梯形![]() 中,AB∥CD,AB⊥BC,CD=2AB=2BC=4,過A點作AE⊥CD,垂足為E,現將ΔADE沿AE折疊,使得DE⊥EC.取AD的中點F,連接BF,CF,EF,如圖乙。
中,AB∥CD,AB⊥BC,CD=2AB=2BC=4,過A點作AE⊥CD,垂足為E,現將ΔADE沿AE折疊,使得DE⊥EC.取AD的中點F,連接BF,CF,EF,如圖乙。
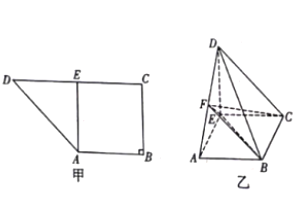
(1)求證:BC⊥平面DEC;
(2)求二面角C-BF-E的余弦值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)先證明DE⊥平面ABCE 可得DE⊥BC,結合BC⊥EC,可證BC⊥平面DEC;
(2)以點E為坐標原點,分別以EA,EC,ED為x,y,z軸建立空間坐標系E-xyz,求出平面EFB和平面BCF的一個法向量,接著代入公式 ,可求得二面角C-BF-E的余弦值.
,可求得二面角C-BF-E的余弦值.
(1)證明:如圖,∵DE⊥EC,DE⊥AE,

∴DE⊥平面ABCE,
又∵BC![]() 平面ABCE,
平面ABCE,
∴DE⊥BC,
又∵BC⊥EC,DE![]() EC=E,
EC=E,
∴BC⊥平面DEC.
(2)如圖,以點E為坐標原點,分別以EA,EC,ED為x,y,z軸建立空間坐標系E-xyz,

∴E(0,0,0),C(0,2,0),B(2,2,0),D(0,0,2),A(2,0,0),F(1,0,1)
設平面EFB的法向量![]()
由![]() ,
, ![]()
所以有
∴取![]() ,得平面EFB的一個法向量
,得平面EFB的一個法向量![]()
設平面BCF的法向量為![]()
由![]() ,
, ![]()
所以有
∴取![]() ,得平面BCF的一個法向量
,得平面BCF的一個法向量![]()
設二面角C-BF-E的大小為![]()
則 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】橢圓![]() 兩焦點分別為
兩焦點分別為![]() 、
、![]() ,且離心率
,且離心率![]() ;
;
(1)設E是直線![]() 與橢圓的一個交點,求
與橢圓的一個交點,求![]() 取最小值時橢圓的方程;
取最小值時橢圓的方程;
(2)已知![]() ,是否存在斜率為k的直線l與(1)中的橢圓交于不同的兩點A、B,使得點N在線段AB的垂直平分線上,若存在,求出直線l在y軸上截距的范圍;若不存在,說明理由。
,是否存在斜率為k的直線l與(1)中的橢圓交于不同的兩點A、B,使得點N在線段AB的垂直平分線上,若存在,求出直線l在y軸上截距的范圍;若不存在,說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (ω>0)的最小正周期為π.
(ω>0)的最小正周期為π.
(Ⅰ)求ω的值和f(x)的單調遞增區間;
(Ⅱ)若關于x的方程f(x)﹣m=0在區間[0,![]() ]上有兩個實數解,求實數m的取值范圍.
]上有兩個實數解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖的程序框圖中,若輸入![]() ,
,![]() ,則輸出的
,則輸出的![]() 值是( )
值是( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/21/1907086498037760/1907898837975040/STEM/25d20caaa911497ea3baaf4f7dee45a3.png]
A. 3 B. 7 C. 11 D. 33
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】阿波羅尼斯(約公元前![]() 年)證明過這樣一個命題:平面內到兩定點距離之比為常數
年)證明過這樣一個命題:平面內到兩定點距離之比為常數![]() 的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.若平面內兩定點
的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.若平面內兩定點![]() 、
、![]() 間的距離為
間的距離為![]() ,動點
,動點![]() 滿足
滿足![]() ,則
,則![]() 的最小值為( )
的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著移動互聯網的快速發展,基于互聯網的共享單車應運而生.某市場研究人員為了了解共享單車運營公司![]() 的經營狀況,對該公司最近六個月(2017年5月到2017年10月)內在西安市的市場占有率進行了統計,并繪制了相應的折線圖.
的經營狀況,對該公司最近六個月(2017年5月到2017年10月)內在西安市的市場占有率進行了統計,并繪制了相應的折線圖.

(1)由拆線圖可以看出,可用線性回歸模型擬合月度市場占有率![]() 與月份代碼
與月份代碼![]() 之間的關系.求
之間的關系.求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)![]() 公司對員工承諾如果公司的共享單車在2017年年底(12月底)能達到西安市場占有率的
公司對員工承諾如果公司的共享單車在2017年年底(12月底)能達到西安市場占有率的![]() ,員工每人都可以獲得年終獎,依據上面計算得到回歸方程估計員工是否能得到年終獎.
,員工每人都可以獲得年終獎,依據上面計算得到回歸方程估計員工是否能得到年終獎.
(參考公式:回歸直線方程為![]() ,其中
,其中
![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高科技公司研究開發了一種新產品,生產這種新產品的每天固定成本為![]() 元,每生產
元,每生產![]() 件,需另投入成本為
件,需另投入成本為![]() 元,
元, 每件產品售價為
每件產品售價為![]() 元(該新產品在市場上供不應求可全部賣完).
元(該新產品在市場上供不應求可全部賣完).
(1)寫出每天利潤![]() 關于每天產量
關于每天產量![]() 的函數解析式;
的函數解析式;
(2)當每天產量為多少件時,該公司在這一新產品的生產中每天所獲利潤最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com