
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100 個網箱,測量各箱水產品的產量(單位:kg).其頻率分布直方圖如下:
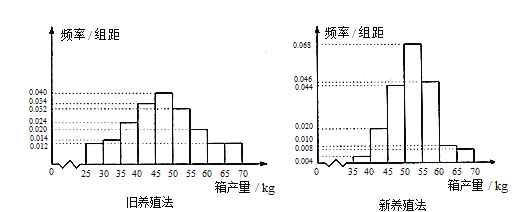
(1)設兩種養殖方法的箱產量相互獨立,記A表示事件:“舊養殖法的箱產量低于50kg,新養殖法的箱產量不低于50kg”,估計A的概率;
(2)填寫下面列聯表,并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關:
箱產量<50kg | 箱產量≥50kg | |
舊養殖法 | ||
新養殖法 |
(3)根據箱產量的頻率分布直方圖,求新養殖法箱產量的中位數的估計值(精確到0.01).
附: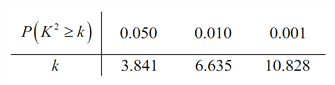 ,
, 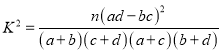
【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]() .
.
【解析】試題分析:(1)利用相互獨立事件概率公式即可求得事件A的概率估計值;(2)寫出列聯表計算![]() 的觀測值,即可確定有99%的把握認為箱產量與養殖方法有關;(3)結合頻率分布直方圖估計中位數為
的觀測值,即可確定有99%的把握認為箱產量與養殖方法有關;(3)結合頻率分布直方圖估計中位數為![]() .
.
試題解析:(1)記B表示事件“舊養殖法的箱產量低于![]() ” ,
” , ![]() 表示事件“新養殖法的箱產量不低于
表示事件“新養殖法的箱產量不低于![]() ”
”
由題意知 ![]()
舊養殖法的箱產量低于![]() 的頻率為
的頻率為
![]()
故![]() 的估計值為0.62
的估計值為0.62
新養殖法的箱產量不低于![]() 的頻率為
的頻率為
![]()
故![]() 的估計值為0.66
的估計值為0.66
因此,事件A的概率估計值為![]()
(2)根據箱產量的頻率分布直方圖得列聯表
箱產量 | 箱產量 | |
舊養殖法 | 62 | 38 |
新養殖法 | 34 | 66 |
![]()
由于![]()
故有![]() 的把握認為箱產量與養殖方法有關.
的把握認為箱產量與養殖方法有關.
(3)因為新養殖法的箱產量頻率分布直方圖中,箱產量低于![]() 的直方圖面積為
的直方圖面積為
![]() ,
,
箱產量低于![]() 的直方圖面積為
的直方圖面積為
![]()
故新養殖法箱產量的中位數的估計值為
![]() .
.
點睛:(1)利用獨立性檢驗,能夠幫助我們對日常生活中的實際問題作出合理的推斷和預測.獨立性檢驗就是考察兩個分類變量是否有關系,并能較為準確地給出這種判斷的可信度,隨機變量的觀測值![]() 值越大,說明“兩個變量有關系”的可能性越大.
值越大,說明“兩個變量有關系”的可能性越大.
(2)利用頻率分布直方圖求眾數、中位數和平均數時,應注意三點:①最高的小長方形底邊中點的橫坐標即眾數;②中位數左邊和右邊的小長方形的面積和是相等的;③平均數是頻率分布直方圖的“重心”,等于頻率分布直方圖中每個小長方形的面積乘以小長方形底邊中點的橫坐標之和.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
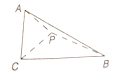
【題目】已知直角三角形![]() 的兩條直角邊
的兩條直角邊![]() ,
, ![]() ,
, ![]() 為斜邊
為斜邊![]() 上一點,沿
上一點,沿![]() 將三角形折成直二面角
將三角形折成直二面角![]() ,此時二面角
,此時二面角![]() 的正切值為
的正切值為![]() ,則翻折后
,則翻折后![]() 的長為( )
的長為( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,且橢圓
,且橢圓![]() 過點
過點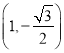 ,記橢圓
,記橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 的點,直線
的點,直線![]() 與直線
與直線![]() 分別交于點
分別交于點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作橢圓
作橢圓![]() 的切線
的切線![]() ,記
,記![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】動圓M與圓(x﹣1)2+y2=1相外切且與y軸相切,則動圓M的圓心的軌跡記C,
(1)求軌跡C的方程;
(2)定點A(3,0)到軌跡C上任意一點的距離|MA|的最小值;
(3)經過定點B(﹣2,1)的直線m,試分析直線m與軌跡C的公共點個數,并指明相應的直線m的斜率k是否存在,若存在求k的取值或取值范圍情況[要有解題過程,沒解題方程只有結論的只得結論分].
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex+ax2-e2x.
(1)若曲線y=f(x)在點(2,f(2))處的切線平行于x軸,求函數f(x)的單調區間;
(2)若x>0時,總有f(x)>-e2x,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩條不重合的直線![]() 和兩個不重合的平面
和兩個不重合的平面![]() ,若
,若![]() ,則下列四個命題:①若
,則下列四個命題:①若![]() ,則
,則![]() ;②若
;②若![]() ,則
,則![]() ; ③若
; ③若![]() ,則
,則![]() ;④若
;④若![]() ,則
,則![]() ,其中正確命題的個數是( )
,其中正確命題的個數是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設二次函數f(x)滿足:對任意x∈R,都有f(x+1)+f(x)=2x2﹣2x﹣3
(1)求f(x)的解析式;
(2)若關于x的方程f(x)=a有兩個實數根x1 , x2 , 且滿足:﹣1<x1<2<x2 , 求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com