
【題目】已知函數![]() 在點
在點![]() 處的切線斜率為0.函數
處的切線斜率為0.函數![]()
(1)試用含![]() 的代數式表示
的代數式表示![]() ;
;
(2)求![]() 的單調區間;
的單調區間;
(3)令![]() ,設函數
,設函數![]() 在
在![]()
![]() 處取得極值,記點
處取得極值,記點![]() ,
,![]() ,證明:線段
,證明:線段![]() 與曲線
與曲線![]() 存在異于
存在異于![]() ,
,![]() 的公共點.
的公共點.
【答案】(1)![]() .(2)答案見解析.(3)證明見解析
.(2)答案見解析.(3)證明見解析
【解析】
(1)求導后利用![]() ,即可得解;
,即可得解;
(2)求導后分![]() ,
,![]() 和
和![]() 三種情況討論求出單調區間即可;
三種情況討論求出單調區間即可;
(3)由![]() 的極值得到
的極值得到![]() ,
,![]() 兩點的坐標,進一步得到直線
兩點的坐標,進一步得到直線![]() 的方程,聯立方程求解即可得解.
的方程,聯立方程求解即可得解.
(1)由![]() ,得
,得![]() ,
,
∵![]() 在點
在點![]() 處的切線斜率為0,
處的切線斜率為0,
∴![]() ,∴
,∴![]() ;
;
(2)由(1)得![]() ,則
,則
![]() ,
,
令![]() ,則
,則![]() 或
或![]() ,
,
①當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,此時
,此時![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,
此時![]() 在
在![]() 和
和![]() 上單調遞增;
上單調遞增;
②當![]() 時,
時,![]() ,此時
,此時![]() 恒成立,且僅有
恒成立,且僅有![]() 時
時![]() ,
,
∴![]() 在
在![]() 上單調遞增;
上單調遞增;
③當![]() 時,
時,![]() ,
,
同理可得![]() 的增區間為
的增區間為![]() 和
和![]() ,單調減區間為
,單調減區間為![]() ;
;
綜上,當![]() 時,
時,![]() 的單調減區間為
的單調減區間為![]() ,單調增區間為
,單調增區間為![]() 和
和![]() ;當
;當![]() 時,
時,![]() 的單調增區間為
的單調增區間為![]() ;當
;當![]() 時,
時,![]() 的單調減區間為
的單調減區間為![]() ,單調增區間為
,單調增區間為![]() 和
和![]() ;
;
(3)當![]() 時,
時,![]() ,
,
令![]() ,則
,則![]() 或
或![]() ,
,
由(2)得![]() 的單調增區間為
的單調增區間為![]() 和
和![]() ,單調減區間為
,單調減區間為![]() ,
,
∴函數![]() 在
在![]() 和3處取得極值,
和3處取得極值,
∴![]() ,
,![]() ,所以
,所以 .
.
∴直線![]() 的方程為
的方程為![]() ,
,
由 得
得![]() ,
,
令![]() ,
,
易得![]() ,
,![]() ,
,
而![]() 的圖象在(0,2)內是一條連續不斷的曲線,
的圖象在(0,2)內是一條連續不斷的曲線,
故![]() 在(0,2)內存在零點
在(0,2)內存在零點![]() ,即線段
,即線段![]() 與曲線
與曲線![]() 有異于
有異于![]() ,
,![]() 的公共點.
的公共點.


科目:高中數學 來源: 題型:
【題目】在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中任選一個,補充在下面的問題中,并解決該問題.
這三個條件中任選一個,補充在下面的問題中,并解決該問題.
已知![]() 的內角
的內角![]() ,
,![]() ,
,![]() 的對邊分別為
的對邊分別為![]() ,
,![]() ,
,![]() ______________,
______________,![]() ,
,![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三個不同平面![]() 、
、![]() 、
、![]() 和直線
和直線![]() ,下面有四個命題:
,下面有四個命題:
①若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
②直線![]() 上有兩點到平面
上有兩點到平面![]() 的距離相等,則
的距離相等,則![]() ;
;
③![]() ,
,![]() ,則
,則![]() ;
;
④若直線![]() 不在平面
不在平面![]() 內,
內,![]() ,
,![]() ,則
,則![]() .
.
則正確命題的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】改編自中國神話故事的動畫電影《哪吒之魔童降世》自7月26日首映,在不到一個月的時間,票房收入就超過了38億元,創造了中國動畫電影的神話.小明和同學相約去電影院觀看《哪吒之魔童降世》,影院的三個放映廳分別在7:30,8:00,8:30開始放映,小明和同學大約在7:40至8:30之間到達影院,且他們到達影院的時間是隨機的,那么他們到達后等待的時間不超過10分鐘的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙十一購物狂歡節,是指每年11月11日的網絡促銷日,源于淘寶商城(天貓)2009年11月11日舉辦的網絡促銷活動,已成為中國電子商務行業的年度盛事.某生產商為了了解其生產的產品在不同電商平臺的銷售情況,統計了![]() 兩個電商平臺各十個網絡銷售店鋪的銷售數據:
兩個電商平臺各十個網絡銷售店鋪的銷售數據:
| 64 | 71 | 81 | 70 | 79 | 69 | 82 | 73 | 75 | 60 |
| 60 | 80 | 97 | 77 | 96 | 87 | 76 | 83 | 94 | 96 |
(1)作出![]() 兩個電商平臺銷售數據的莖葉圖,根據莖葉圖判斷哪個電商平臺的銷售更好,并說明理由;
兩個電商平臺銷售數據的莖葉圖,根據莖葉圖判斷哪個電商平臺的銷售更好,并說明理由;
(2)填寫下面關于店鋪個數的![]() 列聯表,并根據列聯表判斷是否有
列聯表,并根據列聯表判斷是否有![]() 的把握認為銷售量與電商平臺有關;
的把握認為銷售量與電商平臺有關;
銷售量 | 銷售量 | 總計 | |
| |||
| |||
總計 |
(3)生產商要從這20個網絡銷售店鋪銷售量前五名的店鋪中,隨機抽取三個店鋪進行銷售返利,則其中恰好有兩個店鋪的銷售量在95以上的概率是多少?
附: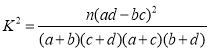 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
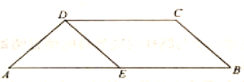
【題目】如圖所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起,使點
折起,使點![]() 到達
到達![]() 的位置,得到如圖所示的四棱錐
的位置,得到如圖所示的四棱錐![]() ,點
,點![]() 為棱
為棱![]() 的中點.
的中點.
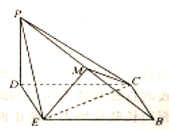
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的左、右焦點分別是
的左、右焦點分別是![]() 、
、![]() ,離心率
,離心率![]() ,過點
,過點![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() 、
、![]() 兩點,
兩點, ![]() 的周長為16.
的周長為16.
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 為原點,圓
為原點,圓![]() :
: ![]() (
(![]() )與橢圓
)與橢圓![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 為橢圓
為橢圓![]() 上一動點,若直線
上一動點,若直線![]() 、
、![]() 與
與![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,求證:
兩點,求證: ![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com