
【題目】已知函數![]() ,
,![]() .
.
(1)若曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,求實教a,b的值.
,求實教a,b的值.
(2)若![]() ,且
,且![]() 對一切正實數x值成立,求實數b的取值范圍.
對一切正實數x值成立,求實數b的取值范圍.
(3)若![]() ,求函數
,求函數![]() 的單調區間.
的單調區間.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)利用導數的幾何意義即可;
(2)分離參數,構造函數,利用導數求出函數的最值即可;
(3)對a分![]() ,
,![]() ,
,![]() ,
,![]() 四種情況討論即可.
四種情況討論即可.
(1)![]() ,由題意
,由題意![]() ,即
,即![]() ,解得
,解得![]() ;
;
(2)當![]() 時,
時,![]() ,
,![]() 對一切正實數x值成立,即
對一切正實數x值成立,即
![]() 對一切正實數x值成立,
對一切正實數x值成立,
設![]() ,則
,則![]() ,由
,由![]() 得
得![]() ,
,
由![]() 得
得![]() ,故
,故![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 單調遞減,
單調遞減,
所以![]() ,所以
,所以![]() ;
;
(3)當![]() 時,
時,![]() ,
,![]() ,
,
令![]()
當![]() 時,由
時,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
當![]() 時,由
時,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
當![]() 時,
時,![]() ,
,
若![]() ,則
,則![]() ,
,![]() ,
,![]() ,所以
,所以![]() 的單調遞增區間為
的單調遞增區間為![]() ,無單調遞減區間;
,無單調遞減區間;
若![]() ,由
,由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
綜上,當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ,無單調遞減區間;
,無單調遞減區間;
當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某地自2014年至2019年每年年初統計所得的人口數量如表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人數(單位:千人) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)根據表中的數據判斷從2014年到2019年哪個跨年度的人口增長數量最大?并描述該地人口數量的變化趨勢;
(2)研究人員用函數![]() 擬合該地的人口數量,其中
擬合該地的人口數量,其中![]() 的單位是年,2014年年初對應時刻
的單位是年,2014年年初對應時刻![]() ,
,![]() 的單位是千人,經計算可得
的單位是千人,經計算可得![]() ,請解釋
,請解釋![]() 的實際意義.
的實際意義.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,△ABC是邊長為6的等邊三角形,D,E分別為AA1,BC的中點.
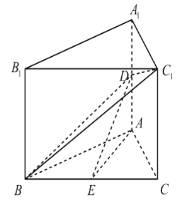
(1)證明:AE//平面BDC1;
(2)若異面直線BC1與AC所成角的余弦值為![]() .求DE與平面BDC1所成角的正弦值.
.求DE與平面BDC1所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)直線![]() 在矩陣
在矩陣![]() 所對應的變換
所對應的變換![]() 下得到直線
下得到直線![]() ,求
,求![]() 的方程.
的方程.
(2)已知點![]() 是曲線
是曲線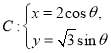 (
(![]() 為參數,
為參數,![]() )上一點,
)上一點,![]() 為坐標原點直線
為坐標原點直線![]() 的傾斜角為
的傾斜角為![]() ,求點
,求點![]() 的坐標.
的坐標.
(3)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張軍自主創業,在網上經營一家干果店,銷售的干果中有松子、開心果、腰果、核桃,價格依次為120元/千克、80元/千克、70元/千克、40元千克,為增加銷量,張軍對這四種干果進行促銷:一次購買干果的總價達到150元,顧客就少付x(2x∈Z)元.每筆訂單顧客網上支付成功后,張軍會得到支付款的80%.
①若顧客一次購買松子和腰果各1千克,需要支付180元,則x=________;
②在促銷活動中,為保證張軍每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值.經數據處理后得到該樣本的頻率分布直方圖,其中質量指標值不大于1.50的莖葉圖如圖所示,以這100件產品的質量指標值在各區間內的頻率代替相應區間的概率.
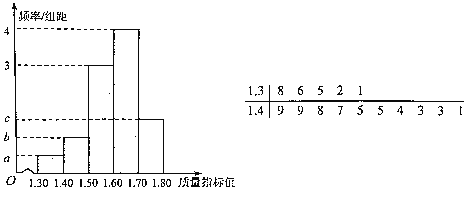
(1)求圖中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估計這種產品質量指標值的平均數及方差(說明:①同一組中的數據用該組區間的中點值作代表;②方差的計算只需列式正確);
(3)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“質量指標值不低于1.50的產品至少要占全部產品的![]() ”的規定?
”的規定?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校在一次期末數學測試中,為統計學生的考試情況,從學校的2000名學生中隨機抽取50名學生的考試成績,被測學生成績全部介于65分到145分之間(滿分150分),將統計結果按如下方式分成八組:第一組![]() ,第二組
,第二組![]() ,…,第八組
,…,第八組![]() ,如圖是按上述分組方法得到的頻率分布直方圖的一部分.
,如圖是按上述分組方法得到的頻率分布直方圖的一部分.
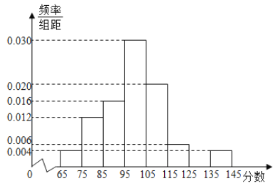
(1)求第七組的頻率;
(2)用樣本數據估計該校的2000名學生這次考試成績的平均分(同一組中的數據用該組區間的中點值代表該組數據平均值);
(3)若從樣本成績屬于第六組和第八組的所有學生中隨機抽取2名,求他們的分差的絕對值小于10分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在點
在點![]() 處的切線斜率為0.函數
處的切線斜率為0.函數![]()
(1)試用含![]() 的代數式表示
的代數式表示![]() ;
;
(2)求![]() 的單調區間;
的單調區間;
(3)令![]() ,設函數
,設函數![]() 在
在![]()
![]() 處取得極值,記點
處取得極值,記點![]() ,
,![]() ,證明:線段
,證明:線段![]() 與曲線
與曲線![]() 存在異于
存在異于![]() ,
,![]() 的公共點.
的公共點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com