
已知函數 , 在
, 在 處取得極小值2.
處取得極小值2.
(1)求函數 的解析式;
的解析式;
(2)求函數 的極值;
的極值;
(3)設函數 , 若對于任意
, 若對于任意 ,總存在
,總存在 , 使得
, 使得 , 求實數
, 求實數  的取值范圍.
的取值范圍.
(1)函數 的解析式為
的解析式為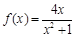 ;(2)
;(2)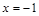 時,函數
時,函數 有極小值-2;當
有極小值-2;當 時,函數
時,函數 有極大值2 ;(3)a的取值范圍是(-∞,-1]∪[ 3,+∞).
有極大值2 ;(3)a的取值范圍是(-∞,-1]∪[ 3,+∞).
解析試題分析:(1)根據函數在極值處導函數為0,極小值為2聯立方程組即可求得m,n;(2)由(1)求得函數解析式,對函數求導且讓導函數為0,即可求得極大值和極小值;(3)依題意只需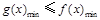 即可,當
即可,當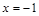 時,函數
時,函數 有最小值-2 ,即對任意
有最小值-2 ,即對任意 總存在
總存在 ,使得
,使得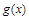 的最小值不大于-2 ;而
的最小值不大于-2 ;而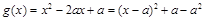 ,分
,分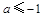 、
、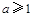 、
、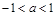 三種情況討論即可.
三種情況討論即可.
試題解析:(1)∵函數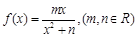 在
在 處取得極小值2,∴
處取得極小值2,∴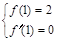 1分
1分
又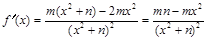 ∴
∴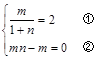
由②式得m=0或n=1,但m=0顯然不合題意 ∴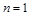 ,代入①式得m=4
,代入①式得m=4
∴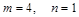 2分
2分
經檢驗,當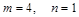 時,函數
時,函數 在
在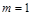 處取得極小值2
處取得極小值2
∴函數 的解析式為
的解析式為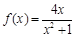 4分
4分
(2)∵函數 的定義域為
的定義域為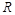 且由(1)有
且由(1)有 
令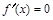 ,解得:
,解得: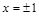
∴當x變化時,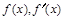 的變化情況如下表:
的變化情況如下表: