
【題目】已知圓 ![]() 的有
的有 ![]() 條弦,且任意兩條弦都彼此相交,任意三條弦不共點,這
條弦,且任意兩條弦都彼此相交,任意三條弦不共點,這 ![]() 條弦將圓
條弦將圓 ![]() 分成了
分成了 ![]() 個區域,(例如:如圖所示,圓
個區域,(例如:如圖所示,圓 ![]() 的一條弦將圓
的一條弦將圓 ![]() 分成了2(即
分成了2(即 ![]() )個區域,圓
)個區域,圓 ![]() 的兩條弦將圓
的兩條弦將圓 ![]() 分成了4(即
分成了4(即 ![]() )個區域,圓
)個區域,圓 ![]() 的3條弦將圓
的3條弦將圓 ![]() 分成了7(即
分成了7(即 ![]() )個區域),以此類推,那么
)個區域),以此類推,那么 ![]() 與
與 ![]()
![]() 之間的遞推式關系為: .
之間的遞推式關系為: . 
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】70年代中期,美國各所名牌大學校園內,人們都像發瘋一般,夜以繼日,廢寢忘食地玩一個數學游戲.這個游戲十分簡單:任意寫出一個自然數N,并且按照以下的規律進行變換:如果是個奇數,則下一步變成3N+1;如果是個偶數,則下一步變成 ![]() .不單單是學生,甚至連教師、研究員、教授與學究都紛紛加入.為什么這個游戲的魅力經久不衰?因為人們發現,無論N是怎樣一個數字,最終都無法逃脫回到谷底1.準確地說,是無法逃出落入底部的4﹣2﹣1循環,永遠也逃不出這樣的宿命.這就是著名的“冰雹猜想”.按照這種運算,自然數27經過十步運算得到的數為( )
.不單單是學生,甚至連教師、研究員、教授與學究都紛紛加入.為什么這個游戲的魅力經久不衰?因為人們發現,無論N是怎樣一個數字,最終都無法逃脫回到谷底1.準確地說,是無法逃出落入底部的4﹣2﹣1循環,永遠也逃不出這樣的宿命.這就是著名的“冰雹猜想”.按照這種運算,自然數27經過十步運算得到的數為( )
A.142
B.71
C.214
D.107
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l與拋物線y2=4x相交于不同的A、B兩點.
(1)如果直線l過拋物線的焦點,求 ![]() ·
· ![]() 的值;
的值;
(2)如果 ![]() ·
· ![]() =-4,證明直線l必過一定點,并求出該定點.
=-4,證明直線l必過一定點,并求出該定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex(sinx+cosx).
(1)如果對于任意的x∈[0, ![]() ],f(x)≥kx+excosx恒成立,求實數k的取值范圍;
],f(x)≥kx+excosx恒成立,求實數k的取值范圍;
(2)若x∈[﹣ ![]() ,
, ![]() ],過點M(
],過點M( ![]() ,0)作函數f(x)的圖象的所有切線,令各切點的橫坐標按從小到大構成數列{xn},求數列{xn}的所有項之和.
,0)作函數f(x)的圖象的所有切線,令各切點的橫坐標按從小到大構成數列{xn},求數列{xn}的所有項之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 過圓
過圓![]() 與直線
與直線![]() 的交點,且圓
的交點,且圓![]() 上任意一點關于直線
上任意一點關于直線![]() 的對稱點仍在圓
的對稱點仍在圓![]() 上.
上.
(1)求圓![]() 的標準方程;
的標準方程;
(2)若圓![]() 與
與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() 兩點(異于點
兩點(異于點![]() ),且點
),且點![]() 滿足
滿足![]() ,
,![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線 ![]() 的焦點為
的焦點為 ![]() ,
, ![]() 是拋物線上橫坐標為4,且位于
是拋物線上橫坐標為4,且位于 ![]() 軸上方的點,
軸上方的點, ![]() 到拋物線準線的距離等于5,過
到拋物線準線的距離等于5,過 ![]() 作
作 ![]() 垂直于
垂直于 ![]() 軸,垂足為
軸,垂足為 ![]() ,
, ![]() 的中點為
的中點為 ![]() .
.
(1)求拋物線的方程;
(2)若過 ![]() 作
作 ![]() ,垂足為
,垂足為 ![]() ,求點
,求點 ![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產某種產品,每生產1噸產品需人工費4萬元,每天還需固定成本3萬元.經過長期調查統計,每日的銷售額![]() (單位:萬元)與日產量
(單位:萬元)與日產量![]() (單位:噸)滿足函數關系
(單位:噸)滿足函數關系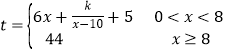 ,已知每天生產4噸時利潤為7萬元.
,已知每天生產4噸時利潤為7萬元.
(1)求![]() 的值;
的值;
(2)當日產量為多少噸時,每天的利潤最大,最大利潤為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com