
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
【答案】(Ⅰ)見解析;(Ⅱ)![]() .
.
【解析】試題分析:本題考查線面平行、線線平行、向量法等基礎知識,考查空間想象能力、分析問題的能力、計算能力.第一問,利用線面平行的定理,先證明線線平行,再證明線面平行;第二問,可以先找到線面角,再在三角形中解出正弦值,還可以用向量法建立直角坐標系解出正弦值.
試題解析:(Ⅰ)在梯形ABCD中,AB與CD不平行.
延長AB,DC,相交于點M(M∈平面PAB),點M即為所求的一個點.理由如下:
由已知,BC∥ED,且BC=ED.
所以四邊形BCDE是平行四邊形.
從而CM∥EB.
又EB![]() 平面PBE,CM
平面PBE,CM![]() 平面PBE,
平面PBE,
所以CM∥平面PBE.
(說明:延長AP至點N,使得AP=PN,則所找的點可以是直線MN上任意一點)
(Ⅱ)方法一:
由已知,CD⊥PA,CD⊥AD,PA![]() AD=A,
AD=A,
所以CD⊥平面PAD.
從而CD⊥PD.
所以![]() PDA是二面角P-CD-A的平面角.
PDA是二面角P-CD-A的平面角.
所以![]() PDA=45°.
PDA=45°.
設BC=1,則在Rt△PAD中,PA=AD=2.
過點A作AH⊥CE,交CE的延長線于點H,連接PH.
易知PA⊥平面ABCD,
從而PA⊥CE.
于是CE⊥平面PAH.
所以平面PCE⊥平面PAH.
過A作AQ⊥PH于Q,則AQ⊥平面PCE.
所以![]() APH是PA與平面PCE所成的角.
APH是PA與平面PCE所成的角.
在Rt△AEH中,![]() AEH=45°,AE=1,
AEH=45°,AE=1,
所以AH=![]() .
.
在Rt△PAH中,PH=![]() =
=![]() ,
,
所以sin![]() APH=
APH=![]() =
=![]() .
.

方法二:
由已知,CD⊥PA,CD⊥AD,PA![]() AD=A,
AD=A,
所以CD⊥平面PAD.
于是CD⊥PD.
從而![]() PDA是二面角P-CD-A的平面角.
PDA是二面角P-CD-A的平面角.
所以![]() PDA=45°.
PDA=45°.
由PA⊥AB,可得PA⊥平面ABCD.
設BC=1,則在Rt△PAD中,PA=AD=2.
作Ay⊥AD,以A為原點,以![]() ,
,![]() 的方向分別為x軸,z軸的正方向,建立如圖所示的空間直角坐標系A-xyz,則A(0,0,0),P(0,0,2),C(2,1,0),E(1,0,0),
的方向分別為x軸,z軸的正方向,建立如圖所示的空間直角坐標系A-xyz,則A(0,0,0),P(0,0,2),C(2,1,0),E(1,0,0),
所以![]() =(1,0,-2),
=(1,0,-2),![]() =(1,1,0),
=(1,1,0),![]() =(0,0,2)
=(0,0,2)
設平面PCE的法向量為n=(x,y,z),
由 得
得![]() 設x=2,解得n=(2,-2,1).
設x=2,解得n=(2,-2,1).
設直線PA與平面PCE所成角為α,則sinα=![]() =
=![]() .
.
所以直線PA與平面PCE所成角的正弦值為![]() .
.



科目:高中數學 來源: 題型:
【題目】設p:A={x|2x2﹣3ax+a2<0},q:B={x|x2+3x﹣10≤0}.
(1)求A;
(2)當a<0時,若¬p是¬q的必要不充分條件,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
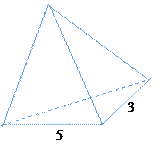
【題目】如圖所示,某幾何體的三視圖都是直角三角形,則該幾何體的體積等于__________.
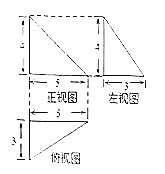
【答案】10
【解析】幾何體為三棱錐,(高為4,底面為直角三角形),體積為![]()
點睛:空間幾何體體積問題的常見類型及解題策略
(1)若所給定的幾何體是可直接用公式求解的柱體、錐體或臺體,則可直接利用公式進行求解.
(2)若所給定的幾何體的體積不能直接利用公式得出,則常用轉換法、分割法、補形法等方法進行求解.
(3)若以三視圖的形式給出幾何體,則應先根據三視圖得到幾何體的直觀圖,然后根據條件求解.
【題型】填空題
【結束】
15
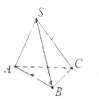
【題目】如圖:在三棱錐![]() 中,已知底面
中,已知底面![]() 是以
是以![]() 為斜邊的等腰直角三角形,且側棱長
為斜邊的等腰直角三角形,且側棱長![]() ,則三棱錐
,則三棱錐![]() 的外接球的表面積等于__________.
的外接球的表面積等于__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4﹣1:幾何證明選講
如圖,⊙O和⊙O′相交于A,B兩點,過A作兩圓的切線分別交兩圓于C、D兩點,連接DB并延長交⊙O于點E.證明:
(1)ACBD=ADAB;
(2)AC=AE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義非零向量![]() 的“相伴函數”為
的“相伴函數”為![]() (
(![]() ),向量
),向量![]() 稱為函數
稱為函數![]() 的“相伴向量”(其中
的“相伴向量”(其中![]() 為坐標原點),記平面內所有向量的“相伴函數”構成的集合為
為坐標原點),記平面內所有向量的“相伴函數”構成的集合為![]() .
.
(1)已知![]() (
(![]() ),求證:
),求證:![]() ,并求函數
,并求函數![]() 的“相伴向量”模的取值范圍;
的“相伴向量”模的取值范圍;
(2)已知點![]() (
(![]() )滿足
)滿足![]() ,向量
,向量![]() 的 “相伴函數”
的 “相伴函數”![]() 在
在![]() 處取得最大值,當點
處取得最大值,當點![]() 運動時,求
運動時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在空間四邊形ABCD中,點E,H分別是邊AB,AD的中點,點F,G分別是邊BC,CD上的點,且![]() ,則下列說法正確的是________.(填寫所有正確說法的序號)
,則下列說法正確的是________.(填寫所有正確說法的序號)

①EF與GH平行; ②EF與GH異面;
③EF與GH的交點M可能在直線AC上,也可能不在直線AC上;
④EF與GH的交點M一定在直線AC上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知函數f(x)=(x+l)lnx﹣ax+a (a為正實數,且為常數)
(1)若f(x)在(0,+∞)上單調遞增,求a的取值范圍;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x∈(0, ![]() ),則函數f(x)=sinxtanx+cosxcotx的值域為( )
),則函數f(x)=sinxtanx+cosxcotx的值域為( )
A.[1,2)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.[1,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com