
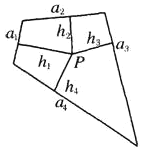
【題目】如圖所示,面積為![]() 的平面凸四邊形的第
的平面凸四邊形的第![]() 條邊的邊長記為
條邊的邊長記為![]() ,此四邊形內任一點
,此四邊形內任一點![]() 到第
到第![]() 條邊的距離記為
條邊的距離記為![]() ,若
,若![]() ,則
,則![]() .類比以上性質,體積為
.類比以上性質,體積為![]() 的三棱錐的第
的三棱錐的第![]() 個面的面積記為
個面的面積記為![]() ,此三棱錐內任一點
,此三棱錐內任一點![]() 到第
到第![]() 個面的距離記為
個面的距離記為![]() ,若
,若![]() ,則
,則![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數(shù)系列答案
同步奧數(shù)系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線;
處的切線;
(2)若函數(shù)![]() 在其定義域內為增函數(shù),求正實數(shù)
在其定義域內為增函數(shù),求正實數(shù)![]() 的取值范圍;
的取值范圍;
(3)設函數(shù)![]() ,若在
,若在![]() 上至少存在一點
上至少存在一點![]() ,使得
,使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知四棱錐![]() ,底面
,底面![]() 為菱形,
為菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 分別是
分別是![]() 的中點。
的中點。

(1)證明:![]() ;
;
(2)若![]() 為
為![]() 上的動點,
上的動點,![]() 與平面
與平面![]() 所成最大角的正切值為
所成最大角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直線![]() 與
與![]() 相交于
相交于![]() 兩點,且滿足:①
兩點,且滿足:①![]() 與
與![]() (
(![]() 為坐標原點)的斜率之和為2;②直線
為坐標原點)的斜率之和為2;②直線![]() 與圓
與圓![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
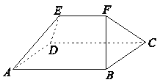
【題目】我國古代數(shù)學名著《九章算術》中記載的“芻甍”(chu meng)是指底面為矩形,頂部只有一條棱的五面體.如圖,五面體![]() 是一個芻甍,其中
是一個芻甍,其中![]() 是正三角形,
是正三角形,![]() ,則以下兩個結論:①
,則以下兩個結論:①![]() ;②
;②![]() ,( )
,( )
A.①和②都不成立B.①成立,但②不成立
C.①不成立,但②成立D.①和②都成立
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖(示意),公路AM、AN圍成的是一塊頂角為鈍角α的角形耕地,其中![]() .在該塊土地中
.在該塊土地中![]() 處有一小型建筑,經測量,它到公路
處有一小型建筑,經測量,它到公路![]() 、
、![]() 的距離
的距離![]() 、
、![]() 分別為
分別為![]() ,
,![]() .現(xiàn)要過點
.現(xiàn)要過點![]() 修建一條直線公路
修建一條直線公路![]() ,將三條公路圍成的區(qū)域
,將三條公路圍成的區(qū)域![]() 建成一個工業(yè)園.設
建成一個工業(yè)園.設![]() ,
,![]()
![]() ,其中
,其中![]() .
.

(1)試建立![]() 間的等量關系;
間的等量關系;
(2)為盡量減少耕地占用,問如何確定B點的位置,使得該工業(yè)園區(qū)的面積最小?并求最小面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
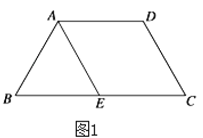
【題目】如圖1,等腰梯形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起后如圖2,使二面角
折起后如圖2,使二面角![]() 成直二面角,設
成直二面角,設![]() 是
是![]() 的中點,
的中點,![]() 是棱
是棱![]() 的中
的中
點.

(1)求證:![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)判斷![]() 能否垂直于平面
能否垂直于平面![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某民營企業(yè)生產A,B兩種產品,根據(jù)市場調查與預測,A產品的利潤y與投資x成正比,其關系如圖甲,B產品的利潤y與投資x的算術平方根成正比,其關系如圖乙![]() 注:利潤與投資單位為萬元
注:利潤與投資單位為萬元![]()
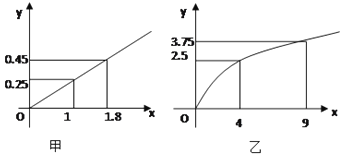
![]() 分別將A,B兩種產品的利潤y表示為投資x的函數(shù)關系式;
分別將A,B兩種產品的利潤y表示為投資x的函數(shù)關系式;
![]() 該企業(yè)已籌集到10萬元資金,并全部投入A,B兩種產品的生產
該企業(yè)已籌集到10萬元資金,并全部投入A,B兩種產品的生產![]() 問:怎樣分配這10萬元資金,才能使企業(yè)獲得最大利潤,最大利潤是多少萬元?
問:怎樣分配這10萬元資金,才能使企業(yè)獲得最大利潤,最大利潤是多少萬元?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com