
【題目】已知p:﹣x2+2x﹣m<0對(duì)x∈R恒成立;q:x2+mx+1=0有兩個(gè)正根.若p∧q為假命題,p∨q為真命題,求m的取值范圍.
【答案】解:若p為真,則△=4﹣4m<0,即m>1
若q為真,則 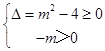 ,即m≤﹣2
,即m≤﹣2
∵p∧q為假命題,p∨q為真命題,則p,q一真一假
若p真q假,則 ![]() ,解得:m>1
,解得:m>1
若p假q真,則 ![]() ,解得:m≤﹣2
,解得:m≤﹣2
綜上所述:m≤﹣2,或m>1
【解析】先確定命題p,q為真時(shí),實(shí)數(shù)m的范圍,進(jìn)而由p∧q為假命題,p∨q為真命題,則p,q一真一假,得到答案.
【考點(diǎn)精析】解答此題的關(guān)鍵在于理解命題的真假判斷與應(yīng)用的相關(guān)知識(shí),掌握兩個(gè)命題互為逆否命題,它們有相同的真假性;兩個(gè)命題為互逆命題或互否命題,它們的真假性沒(méi)有關(guān)系.


 津橋教育計(jì)算小狀元系列答案
津橋教育計(jì)算小狀元系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(Ⅱ)是否存在正整數(shù)![]() ,使得
,使得![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的最大值并給出推導(dǎo)過(guò)程,若不存在,說(shuō)明理由.
的最大值并給出推導(dǎo)過(guò)程,若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,將△ABD沿BD折起,使平面ABD⊥平面BCD,構(gòu)成四面體A﹣BCD,則在四面體ABCD中,下列結(jié)論正確的是( ) 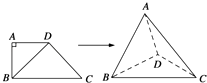
A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2015男籃亞錦賽決賽階段,中國(guó)男籃以![]() 連勝的不敗成績(jī)贏得第
連勝的不敗成績(jī)贏得第![]() 屆亞錦賽冠軍,同時(shí)拿到亞洲唯一
屆亞錦賽冠軍,同時(shí)拿到亞洲唯一![]() 張直通里約奧運(yùn)會(huì)的入場(chǎng)券.賽后,中國(guó)男籃主力易建聯(lián)榮膺本屆亞錦賽
張直通里約奧運(yùn)會(huì)的入場(chǎng)券.賽后,中國(guó)男籃主力易建聯(lián)榮膺本屆亞錦賽![]() (最有價(jià)值球員),下表是易建聯(lián)在這
(最有價(jià)值球員),下表是易建聯(lián)在這![]() 場(chǎng)比賽中投籃的統(tǒng)計(jì)數(shù)據(jù).
場(chǎng)比賽中投籃的統(tǒng)計(jì)數(shù)據(jù).
比分 | 易建聯(lián)技術(shù)統(tǒng)計(jì) | |||
投籃命中 | 罰球命中 | 全場(chǎng)得分 | 真實(shí)得分率 | |
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真實(shí)得分率)是衡量球員進(jìn)攻的效率,其計(jì)算公式為:
(真實(shí)得分率)是衡量球員進(jìn)攻的效率,其計(jì)算公式為:
![]()
(1)從上述![]() 場(chǎng)比賽中隨機(jī)選擇一場(chǎng),求易建聯(lián)在該場(chǎng)比賽中
場(chǎng)比賽中隨機(jī)選擇一場(chǎng),求易建聯(lián)在該場(chǎng)比賽中![]() 超過(guò)
超過(guò)![]() 的概率;
的概率;
(2)我們把比分分差不超過(guò)![]() 分的比賽稱(chēng)為“膠著比賽”.為了考驗(yàn)求易建聯(lián)在“膠著比賽”中的發(fā)揮情況,從“膠著比賽”中隨機(jī)選擇兩場(chǎng),求易建聯(lián)在這兩場(chǎng)比賽中
分的比賽稱(chēng)為“膠著比賽”.為了考驗(yàn)求易建聯(lián)在“膠著比賽”中的發(fā)揮情況,從“膠著比賽”中隨機(jī)選擇兩場(chǎng),求易建聯(lián)在這兩場(chǎng)比賽中![]() 至少有一場(chǎng)超過(guò)
至少有一場(chǎng)超過(guò)![]() 的概率;
的概率;
(3)用![]() 來(lái)表示易建聯(lián)某場(chǎng)的得分,用
來(lái)表示易建聯(lián)某場(chǎng)的得分,用![]() 來(lái)表示中國(guó)隊(duì)該場(chǎng)的總分,畫(huà)出散點(diǎn)圖如圖所示,請(qǐng)根據(jù)散點(diǎn)圖判斷
來(lái)表示中國(guó)隊(duì)該場(chǎng)的總分,畫(huà)出散點(diǎn)圖如圖所示,請(qǐng)根據(jù)散點(diǎn)圖判斷![]() 與
與![]() 之間是否具有線性相關(guān)關(guān)系?結(jié)合實(shí)際簡(jiǎn)單說(shuō)明理由.
之間是否具有線性相關(guān)關(guān)系?結(jié)合實(shí)際簡(jiǎn)單說(shuō)明理由.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知定點(diǎn)![]() ,定直線
,定直線![]() :
: ![]() ,動(dòng)圓
,動(dòng)圓![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ,且與直線
,且與直線![]() 相切.
相切.
(Ⅰ)求動(dòng)圓![]() 的圓心軌跡
的圓心軌跡![]() 的方程;
的方程;
(Ⅱ)過(guò)點(diǎn)![]() 的直線與曲線
的直線與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點(diǎn),分別過(guò)點(diǎn)
兩點(diǎn),分別過(guò)點(diǎn)![]() ,
, ![]() 作曲線
作曲線![]() 的切線
的切線![]() ,
, ![]() ,兩條切線相交于點(diǎn)
,兩條切線相交于點(diǎn)![]() ,求
,求![]() 外接圓面積的最小值.
外接圓面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在銳角△ABC中,a,b,c分別為角A,B,C的對(duì)邊,且4sin2 ![]() ﹣cos2A=
﹣cos2A= ![]() .
.
(1)求角A的大小;
(2)若BC邊上高為1,求△ABC面積的最小值?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)點(diǎn)P在曲線 ![]() 上,點(diǎn)Q在曲線y=ln(2x)上,則|PQ|最小值為( )
上,點(diǎn)Q在曲線y=ln(2x)上,則|PQ|最小值為( )
A.1﹣ln2
B.![]()
C.1+ln2
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]()
(Ⅰ)若函數(shù)![]() 的圖像在點(diǎn)
的圖像在點(diǎn)![]() 處的切線與直線
處的切線與直線![]() 平行,求實(shí)數(shù)
平行,求實(shí)數(shù)![]() 的值;
的值;
(Ⅱ)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅲ)若在函數(shù)![]() 定義域內(nèi),總有
定義域內(nèi),總有![]() 成立,試求實(shí)數(shù)
成立,試求實(shí)數(shù)![]() 的最大值.
的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com