
【題目】已知a>0,b>0,a+b=4,m∈R.
(1)求![]() +
+![]() 的最小值;
的最小值;
(2)若|x+m|![]() |x
|x![]() 2|≤
2|≤![]() +
+![]() 對任意的實數x恒成立,求m的范圍.
對任意的實數x恒成立,求m的范圍.
【答案】(1)1;(2)-3≤m≤1
【解析】
(1)結合條件構造均值定理的結構形式,利用均值定理求解最小值;
(2)根據第(1)問可得![]() +
+![]() 的最小值,求|x+m|
的最小值,求|x+m|![]() |x
|x![]() 2|的最大值小于等于
2|的最大值小于等于![]() +
+![]() 的最小值.
的最小值.
(1)∵a>0,b>0,a+b=4,
∴![]() +
+![]() =(
=(![]() +
+![]() )
)![]() (a+b)=
(a+b)=![]() (2+
(2+![]() +
+![]() )≥
)≥![]() (2+2
(2+2![]() )=1,
)=1,
當且僅當a=b=2時取“=”;∴![]() +
+![]() 的最小值為1;
的最小值為1;
(2)若|x+m|![]() |x-2|≤
|x-2|≤![]() +
+![]() 對任意的實數x恒成立,
對任意的實數x恒成立,
則|x+m|![]() |x-2|≤
|x-2|≤![]() 對任意的實數x恒成立,
對任意的實數x恒成立,
即|x+m|![]() |x-2|≤1對任意的實數x恒成;
|x-2|≤1對任意的實數x恒成;
∵|x+m|![]() |x-2|≤|(x+m)
|x-2|≤|(x+m)![]() (x-2)|=|m+2|,
(x-2)|=|m+2|,
即|m+2|≤1,∴-1≤m+2≤1,解得![]() 3≤m≤
3≤m≤![]() 1,
1,
∴m的取值范圍是![]() 3≤m≤
3≤m≤![]() 1.
1.


 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() 、
、![]() ,
,![]() ,點
,點![]() 在橢圓上,且
在橢圓上,且![]() 的周長為
的周長為![]()
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若點![]() 的坐標為
的坐標為![]() ,不過原點
,不過原點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,設線段
兩點,設線段![]() 的中點為
的中點為![]() ,點
,點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,且
,且![]() ,
,![]() ,
,![]() 三點共線,求
三點共線,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】4月23日是“世界讀書日”,某中學在此期間開展了一系列的讀書教育活動,為了解本校學生課外閱讀情況,學校隨機抽取了100名學生對其課外閱讀時間進行調查,下圖是根據調查結果繪制的學生日均課外閱讀時間(單位:分鐘)的頻率分布直方圖,若將日均課外閱讀時間不低于60分鐘的學生稱為“讀書謎”,低于60分鐘的學生稱為“非讀書謎”.
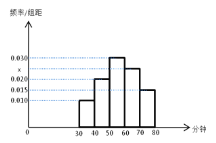
(1)求![]() 的值并估計全校3000名學生中讀書謎大概有多少名?(將頻率視為概率)
的值并估計全校3000名學生中讀書謎大概有多少名?(將頻率視為概率)
(2)根據已知條件完成下面![]() 的列聯表,并據此判斷是否有
的列聯表,并據此判斷是否有![]() 的把握認為“讀書謎”與性別有關?
的把握認為“讀書謎”與性別有關?
非讀書迷 | 讀書迷 | 合計 | |
男 | 40 | ||
女 | 25 | ||
合計 |
附: ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了推動數學教學方法的改革,學校將高一年級部分生源情況基本相同的學生分成甲乙兩個班,每班各40人,甲班按原有模式教學,乙班實施教學方法改革.經過一年的教學實驗,將甲乙兩個班學生一年來的數學成績取平均數,兩個班學生的平均成績均在![]() ,按照區間
,按照區間![]() ,
,![]() ,
,![]() 進行分組,繪制成如下頻率分布直方圖,規定不低于80分(百分制)為優秀.
進行分組,繪制成如下頻率分布直方圖,規定不低于80分(百分制)為優秀.
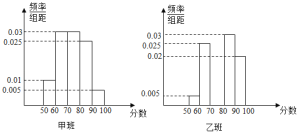
(1)完成表格,并判斷是否有90%以上的把握認為“數學成績優秀與教學改革有關”;
甲班 | 乙班 | 總計 | |
大于等于80分的人數 | |||
小于80分的人數 | |||
總計 |
(2)從乙班![]() 分數段中,按分層抽樣隨機抽取7名學生座談,從中選三位同學發言,記來自
分數段中,按分層抽樣隨機抽取7名學生座談,從中選三位同學發言,記來自![]() 發言的人數為隨機變量
發言的人數為隨機變量![]() ,求
,求![]() 的分布列和期望.附:
的分布列和期望.附: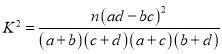 ,
,
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“一本書,一碗面,一條河,一座橋”曾是蘭州的城市名片,而現在“蘭州馬拉松”又成為了蘭州的另一張名片,隨著全民運動健康意識的提高,馬拉松運動不僅在蘭州,而且在全國各大城市逐漸興起,參與馬拉松訓練與比賽的人口逐年增加.為此,某市對人們參加馬拉松運動的情況進行了統計調查.其中一項調查是調查人員從參與馬拉松運動的人中隨機抽取200人,對其每周參與馬拉松長跑訓練的天數進行統計,得到以下統計表:
平均每周進行長跑訓練天數 | 不大于2天 | 3天或4天 | 不少于5天 |
人數 | 30 | 130 | 40 |
若某人平均每周進行長跑訓練天數不少于5天,則稱其為“熱烈參與者”,否則稱為“非熱烈參與者”.
(1)經調查,該市約有2萬人參與馬拉松運動,試估計其中“熱烈參與者”的人數;
(2)根據上表的數據,填寫下列2×2列聯表,并通過計算判斷是否能在犯錯誤的概率不超過0.01的前提下認為“熱烈參與馬拉松”與性別有關?
熱烈參與者 | 非熱烈參與者 | 合計 | |
男 | 140 | ||
女 | 55 | ||
合計 |
附:k2=![]() (n為樣本容量)
(n為樣本容量)
P(k2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】當前全世界人民越來越關注環境保護問題,某地某監測站點于2018年8月起連續n天監測空氣質量指數(AQI),數據統計如下表:
空氣質量指數(μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] |
空氣質量等級 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 |
天數 | 20 | 40 | m | 10 | 5 |
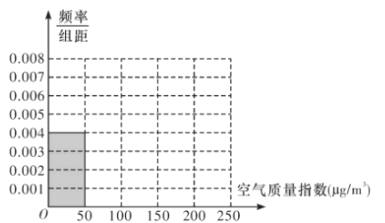
(1)根據所給統計表和頻率分布直方圖中的信息求出n,m的值,并完成頻率分布直方圖;
(2)由頻率分布直方圖,求該組數據的平均數與中位數;
(3)在空氣質量指數分別為[0,50]和(50,100]的監測數據中,用分層抽樣的方法抽取6天,從中任意選取2天,求事件A“兩天空氣質量等級都為良”發生的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖四邊形ABCD為菱形,G為AC與BD交點,面![]() 平面ABCD.
平面ABCD.
(1)證明:![]() 平面BDE;
平面BDE;
(2)若![]() 為等邊三角形,
為等邊三角形,![]() ,
,![]() ,三棱錐
,三棱錐![]() 的體積為
的體積為![]() ,求四棱錐
,求四棱錐![]() 的側面積.
的側面積.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的四個頂點組成的四邊形的面積為
的四個頂點組成的四邊形的面積為![]() ,且經過點
,且經過點 .
.

(1)求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 的下頂點為
的下頂點為![]() ,如圖所示,點
,如圖所示,點![]() 為直線
為直線![]() 上的一個動點,過橢圓
上的一個動點,過橢圓![]() 的右焦點
的右焦點![]() 的直線
的直線![]() 垂直于
垂直于![]() ,且與
,且與![]() 交于
交于![]() 兩點,與
兩點,與![]() 交于點
交于點![]() ,四邊形
,四邊形![]() 和
和![]() 的面積分別為
的面積分別為![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com