
【題目】已知實數![]() ,函數
,函數![]() 在區間
在區間![]() 上的最大值是2,則
上的最大值是2,則![]() ______
______
【答案】![]() 或
或![]()
【解析】
由題意可得f(0)≤2,求得a的范圍,去掉一個絕對值,再由最值的取得在頂點和端點處,計算得a的值,再檢驗可得a的值.
因為函數f(x)=|x2+|x﹣a|﹣3|在區間[﹣1,1]上的最大值是2,可得f(0)≤2,
且a>0,得|a﹣3|≤2,解得1≤a≤5,即有f(x)=|x2﹣x+a﹣3|,﹣1≤x≤1,
由f(x)的最大值在頂點或端點處取得,
當f(﹣1)=2,即|a﹣1|=2,解得a=3或﹣1(舍去);
當f(1)=2,即|a﹣3|=2,解得a=5或a=1;
當f(![]() )=2,即|a﹣
)=2,即|a﹣![]() |=2,解得a=
|=2,解得a=![]() 或
或![]() (舍去).
(舍去).
當a=1時,f(x)=|x2﹣x﹣2|,因為f(![]() )=
)=![]() >2,不符題意;(舍去).
>2,不符題意;(舍去).
當a=5時,f(x)=|x2﹣x+2|,因為f(-1)=4>2,不符題意;(舍去).
當a=3時,f(x)=|x2﹣x|,顯然當x=﹣1時,取得最大值2,符合題意;
當a=![]() 時,f(x)=|x2﹣x﹣
時,f(x)=|x2﹣x﹣![]() |,f(1)=
|,f(1)=![]() ,f(﹣1)=
,f(﹣1)=![]() ,f(
,f(![]() )=2,符合題意.
)=2,符合題意.
故答案為:3或![]() .
.


科目:高中數學 來源: 題型:
【題目】某小區為了調查居民的生活水平,隨機從小區住戶中抽取![]() 個家庭,得到數據如下:
個家庭,得到數據如下:
家庭編號 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x(千元) | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y(千元) | 4 | 5 | 6 | 8 | 8 | 11 |
參考公式:回歸直線的方程是:![]() ,其中,
,其中,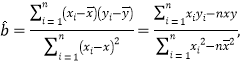
![]() .
.
(1)據題中數據,求月支出![]() (千元)關于月收入
(千元)關于月收入![]() (千元)的線性回歸方程(保留一位小數);
(千元)的線性回歸方程(保留一位小數);
(2)從這![]() 個家庭中隨機抽取
個家庭中隨機抽取![]() 個,求月支出都少于
個,求月支出都少于![]() 萬元的概率.
萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應黨中央號召,學校以“我們都是追夢人”為主題舉行知識競賽。現有10道題,其中6道甲類題,4道乙類題,王同學從中任取3道題解答.
(Ⅰ)求王同學至少取到2道乙類題的概率;
(Ⅱ)如果王同學答對每道甲類題的概率都是![]() ,答對每道乙類題的概率都是
,答對每道乙類題的概率都是![]() ,且各題答對與否相互獨立,已知王同學恰好選中2道甲類題,1道乙類題,用
,且各題答對與否相互獨立,已知王同學恰好選中2道甲類題,1道乙類題,用![]() 表示王同學答對題的個數,求隨機變量
表示王同學答對題的個數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產并銷售某高科技產品,已知每年生產該產品的固定成本是800萬元,生產成本e(單位;萬元)與生產的產品件數x(單位:萬件)的平方成正比;該產品單價p(單位:元)與生產的產品件數x滿足![]() (b為常數),已知當該產品的單價為300元時,生產成本是1800萬元,當單價為320元時,生產成本是200萬元,且工廠生產的產品都可以銷售完.
(b為常數),已知當該產品的單價為300元時,生產成本是1800萬元,當單價為320元時,生產成本是200萬元,且工廠生產的產品都可以銷售完.
(1)每年生產該產品多少萬件時,平均成本最低,最低為多少?
(2)若該工廠希望年利潤不低于8200萬元,則每年大約應該生產多少萬件該產品?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(1),在直角梯形![]() 中,
中,![]() 為
為![]() 的中點,四邊形
的中點,四邊形![]() 為正方形,將
為正方形,將![]() 沿
沿![]() 折起,使點
折起,使點![]() 到達點
到達點![]() ,如圖(2),
,如圖(2),![]() 為
為![]() 的中點,且
的中點,且![]() ,點
,點![]() 為線段
為線段![]() 上的一點.
上的一點.

(1)證明:![]() ;
;
(2)當![]() 與
與![]() 夾角最小時,求平面
夾角最小時,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知球的半徑為4,球面被互相垂直的兩個平面所截,得到的兩個圓的公共弦長為2![]() .若球心到這兩個平面的距離相等,則這兩個圓的半徑之和為( )
.若球心到這兩個平面的距離相等,則這兩個圓的半徑之和為( )
A. 4B. 6C. 8D. 10
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列條件:①焦點在![]() 軸上;②焦點在
軸上;②焦點在![]() 軸上;③拋物線上橫坐標為
軸上;③拋物線上橫坐標為![]() 的點
的點![]() 到其焦點
到其焦點![]() 的距離等于
的距離等于![]() ;④拋物線的準線方程是
;④拋物線的準線方程是![]() .
.
(1)對于頂點在原點![]() 的拋物線
的拋物線![]() :從以上四個條件中選出兩個適當的條件,使得拋物線
:從以上四個條件中選出兩個適當的條件,使得拋物線![]() 的方程是
的方程是![]() ,并說明理由;
,并說明理由;
(2)過點![]() 的任意一條直線
的任意一條直線![]() 與
與![]() 交于
交于![]() ,
,![]() 不同兩點,試探究是否總有
不同兩點,試探究是否總有![]() ?請說明理由.
?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com