
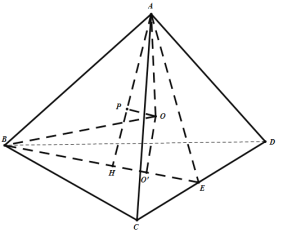
【題目】在四面體![]() 中,已知
中,已知![]() ,
,![]() .
.
(1)當四面體體積最大時,求![]() 的值;
的值;
(2)當![]() 時,設四面體
時,設四面體![]() 的外接球球心為
的外接球球心為![]() ,求
,求![]() 和平面
和平面![]() 所成夾角的正弦值.
所成夾角的正弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,過點
,過點![]() 作
作![]() ,由題意可知當
,由題意可知當![]() 平面
平面![]() 時,四面體的面積最大,求出此時的
時,四面體的面積最大,求出此時的![]() 的值即可得解;
的值即可得解;
(2)在線段![]() 上取
上取![]() ,使
,使![]() ,
,![]() 為
為![]() 的內心,過
的內心,過![]() 作
作![]() 平面
平面![]() ,則球心在直線
,則球心在直線![]() 上,設
上,設![]() ,球的半徑為
,球的半徑為![]() ,由勾股定理求得
,由勾股定理求得![]() 后,由
后,由![]() 即可得解.
即可得解.
(1)取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,過點
,過點![]() 作
作![]() ,
,
由![]() 可得
可得![]() ,
,![]() ,
,![]() ,
,
由![]() 可得
可得![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
即![]() 即為四面體的高,由
即為四面體的高,由![]() ,可知當
,可知當![]() 平面
平面![]() 四面體面積最大,
四面體面積最大,
此時![]() 即
即![]() 的值為
的值為![]() ;
;
(2)當![]() 時,
時,![]() ,則
,則![]() 為
為![]() 的中點,
的中點,
所以![]() ,
,![]() ,
,
在線段![]() 上取
上取![]() ,使
,使![]() ,易知
,易知![]() 為
為![]() 的內心,
的內心,![]() ,
,
過![]() 作
作![]() 平面
平面![]() ,則球心在直線
,則球心在直線![]() 上,
上,
球心為![]() ,過點
,過點![]() 作
作![]() ,連接
,連接![]() ,
,![]() ,則
,則![]() ,
,
設![]() ,球的半徑為
,球的半徑為![]() ,則
,則![]() ,
,
則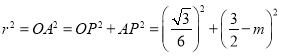 ,
,
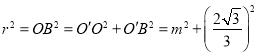 ,
,
所以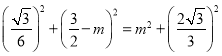 ,解得
,解得![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
設![]() 和平面
和平面![]() 所成夾角為
所成夾角為![]() ,
,
由![]() 平面
平面![]() 可知
可知![]() ,
,
所以![]() 和平面
和平面![]() 所成夾角的正弦值為
所成夾角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為:
的參數方程為:![]() (
(![]() 為參數),
為參數),![]() 的參數方程為:
的參數方程為:![]() (
(![]() 為參數).
為參數).
(1)化![]() 、
、![]() 的參數方程為普通方程,并說明它們分別表示什么曲線;
的參數方程為普通方程,并說明它們分別表示什么曲線;
(2)若直線![]() 的極坐標方程為:
的極坐標方程為:![]() ,曲線
,曲線![]() 上的點
上的點![]() 對應的參數
對應的參數![]() ,曲線
,曲線![]() 上的點
上的點![]() 對應的參數
對應的參數![]() ,求
,求![]() 的中點
的中點![]() 到直線
到直線![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 上單調遞增,求實數
上單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(2)若函數![]() 有兩個不同的零點
有兩個不同的零點![]() .
.
(ⅰ)求實數![]() 的取值范圍;
的取值范圍;
(ⅱ)求證:![]() .(其中
.(其中![]() 為
為![]() 的極小值點)
的極小值點)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體![]() 的棱長為1,P是空間中任意一點,下列正確命題的個數是( )
的棱長為1,P是空間中任意一點,下列正確命題的個數是( )
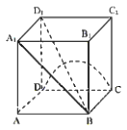
①若P為棱![]() 中點,則異面直線AP與CD所成角的正切值為
中點,則異面直線AP與CD所成角的正切值為![]() ;
;
②若P在線段![]() 上運動,則
上運動,則![]() 的最小值為
的最小值為![]() ;
;
③若P在半圓弧CD上運動,當三棱錐![]() 的體積最大時,三棱錐
的體積最大時,三棱錐![]() 外接球的表面積為
外接球的表面積為![]() ;
;
④若過點P的平面![]() 與正方體每條棱所成角相等,則
與正方體每條棱所成角相等,則![]() 截此正方體所得截面面積的最大值為
截此正方體所得截面面積的最大值為![]()
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中點(如圖1),將
是EA的中點(如圖1),將![]() 沿CD折起到圖2中
沿CD折起到圖2中![]() 的位置,得到四棱錐是
的位置,得到四棱錐是![]() .
.
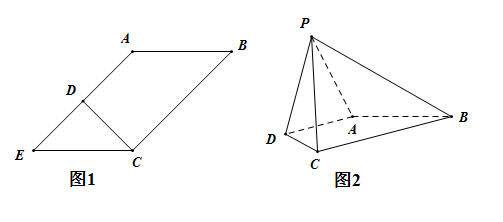
(1)求證:![]() 平面PDA;
平面PDA;
(2)若PD與平面ABCD所成的角為![]() .且
.且![]() 為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了政府對過熱的房地產市場進行調控決策,統計部門對城市人和農村人進行了買房的心理預期調研,用簡單隨機抽樣的方法抽取110人進行統計,得到如下列聯表:
買房 | 不買房 | 糾結 | |
城市人 | 5 | 15 | |
農村人 | 20 | 10 |
已知樣本中城市人數與農村人數之比是3:8.
![]() 分別求樣本中城市人中的不買房人數和農村人中的糾結人數;
分別求樣本中城市人中的不買房人數和農村人中的糾結人數;
![]() 用獨立性檢驗的思想方法說明在這三種買房的心理預期中哪一種與城鄉有關?
用獨立性檢驗的思想方法說明在這三種買房的心理預期中哪一種與城鄉有關?
參考公式:![]() .
.
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() (
(![]() 為常數)對于任意的
為常數)對于任意的![]() 恒成立.
恒成立.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)證明:數列![]() 是等差數列;
是等差數列;
(3)若![]() ,關于
,關于![]() 的不等式
的不等式![]() 有且僅有兩個不同的整數解,求
有且僅有兩個不同的整數解,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 分別在
分別在![]() 軸,
軸,![]() 軸上運動,
軸上運動,![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() ,若直線
,若直線![]() ,
,![]() 的斜率之和為2,直線
的斜率之和為2,直線![]() 是否恒過定點?若是,求出定點的坐標;若不是,請說明理由.
是否恒過定點?若是,求出定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的非負半軸為極軸且取相同的單位長度建立極坐標系,圓
軸的非負半軸為極軸且取相同的單位長度建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與圓
的普通方程與圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設動點![]() 在圓
在圓![]() 上,動線段
上,動線段![]() 的中點
的中點![]() 的軌跡為
的軌跡為![]() ,
,![]() 與直線
與直線![]() 交點為
交點為![]() ,且直角坐標系中,
,且直角坐標系中,![]() 點的橫坐標大于
點的橫坐標大于![]() 點的橫坐標,求點
點的橫坐標,求點![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com