
���}Ŀ����֪��(sh��)��![]() �M(m��n)��
�M(m��n)��![]() ��
��![]() ���O(sh��)
���O(sh��)![]() ��
��![]() .
.
��1����![]() ��
��
��2����![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��3���� .
.
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ��
��![]() ����3��
����3��![]() .
.
��������
��1�����δ���Ӌ(j��)�㣬�����![]() ��
��
��2���w�{��![]() ������(sh��)�W(xu��)�w�{���C����
������(sh��)�W(xu��)�w�{���C����
��3�������(xi��ng)���������![]() ��Ȼ����O�ޣ�
��Ȼ����O�ޣ�
��1����![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��2���ɣ�1���w�{��![]() ��
��
������(sh��)�W(xu��)�w�{���C����
1��n=1��n=2�r(sh��)���ɣ�1��֪������
2����O(sh��)n=k��k>1���r(sh��)���Y(ji��)Փ��������bk=2k2��
�tn=k+1�r(sh��)��ak=bk-k=2k2-k��![]() ��
��
ak+1=(2k+1)(k+1)��
��bk+1=ak+1+(k+1)=(2k+1)(k+1)+(k+1)=2(k+1)2��
��n=k+1�r(sh��)�Y(ji��)Փ������
����(du��)����������(sh��)n��bn=2n2��
��3���ɣ�2��֪n![]() 2�r(sh��)��
2�r(sh��)��![]() ��
��
��![]()
![]()
![]() ��
��
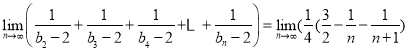
![]() ��
��


 ��У��������ĩ�_�̾�ϵ�д�
��У��������ĩ�_�̾�ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ijУ�ĸ߶��꼉(j��)�W(xu��)�����S�C(j��)��ȡ100���W(xu��)����������ij�ο�ԇ�Ĕ�(sh��)�W(xu��)�ɿ�(j��)����������(sh��)���ֳ����Σ�[40��50����[50��60��������[90��100]��õ��l�ʷֲ�ֱ���D����D��ʾ����
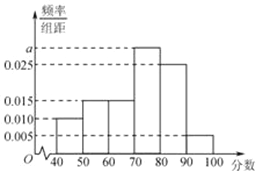
��1�����?j��n)?sh��)��[70��80���е��˔�(sh��)��
��2�����÷ӳ�ӵķ����ķ�?j��n)?sh��)��[40��50����[50��60���ČW(xu��)���й���ȡ5 �ˣ�ԓ5 ���гɿ�(j��)?c��)?/span>[40��50�����Ў�����
��3���ڣ�2���г�ȡ��5���У��S�C(j��)�xȡ2 �ˣ����?j��n)?sh��)��[40��50����[50��60����1 �˵ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���タ(xi��n)![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() ���ҽ��c(di��n)��F��ֱ��(xi��n)l�c���タ(xi��n)�ཻ��A��B���c(di��n)��
���ҽ��c(di��n)��F��ֱ��(xi��n)l�c���タ(xi��n)�ཻ��A��B���c(di��n)��
�����タ(xi��n)C�ķ��̣��������(zh��n)��(xi��n)���̣�
��![]() ������(bi��o)ԭ�c(di��n).��
������(bi��o)ԭ�c(di��n).��![]() ���C��ֱ��(xi��n)l���^(gu��)һ���c(di��n)�������ԓ���c(di��n)��
���C��ֱ��(xi��n)l���^(gu��)һ���c(di��n)�������ԓ���c(di��n)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() ����
���� ![]() ����
����![]() ��
��
��������(d��ng)![]() �r(sh��)���C����ƽ��
�r(sh��)���C����ƽ��![]() ƽ��
ƽ��![]() ��
��
��������(d��ng)�����F![]() ���w�e��
���w�e��![]() ���Ҷ����
���Ҷ����![]() ���g�Ǖr(sh��)����ֱ��(xi��n)
���g�Ǖr(sh��)����ֱ��(xi��n)![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ڡ�ABC��,߅a��b��c�քe�ǽ�A��B��C�Č�(du��)߅,�ҝM(m��n)��bcosC=(3a-c)cosB
(1)��cosB
(2)����ABC����e��4![]() ,b=4
,b=4![]() ,���ABC�����L(zh��ng)
,���ABC�����L(zh��ng)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������С�}�M(m��n)��12�֣�
��֪���タ(xi��n)C�ķ���C��y2="2" p x��p��0���^(gu��)�c(di��n)A��1��-2��.
��I�����タ(xi��n)C�ķ��̣��������(zh��n)��(xi��n)���̣�
��II���Ƿ����ƽ����OA��O������(bi��o)ԭ�c(di��n)����ֱ��(xi��n)l��ʹ��ֱ��(xi��n)l�c���タ(xi��n)C�й����c(di��n)����ֱ��(xi��n)OA�cl�ľ��x����![]() �������ڣ����ֱ��(xi��n)l�ķ��̣��������ڣ��f(shu��)�����ɡ�
�������ڣ����ֱ��(xi��n)l�ķ��̣��������ڣ��f(shu��)�����ɡ�
���𰸡���I�����タ(xi��n)C�ķ��̞�![]() �����(zh��n)��(xi��n)���̞�
�����(zh��n)��(xi��n)���̞�![]() ��II�������}���ֱ��(xi��n)l ���ڣ��䷽�̞�2x+y-1 =0.
��II�������}���ֱ��(xi��n)l ���ڣ��䷽�̞�2x+y-1 =0.
��������
ԇ�}���������タ(xi��n)��(bi��o)��(zh��n)���̣�һ�����ô���ϵ��(sh��)����ֻ��һ��(g��)��(d��)���l���_��p��ֵ������2��2��2p��1������p��2�����ɒ��タ(xi��n)���̴_�����(zh��n)��(xi��n)���̣�![]() �����������}���O(sh��)
�����������}���O(sh��)![]() ��
��![]() ������ֱ��(xi��n)OA�c
������ֱ��(xi��n)OA�c![]() �ľ��x����
�ľ��x����![]() ����(j��)�ɗlƽ�о�(xi��n)���x��ʽ�ã�
����(j��)�ɗlƽ�о�(xi��n)���x��ʽ�ã�![]() ���
���![]() ���ٸ���(j��)ֱ��(xi��n)
���ٸ���(j��)ֱ��(xi��n)![]() �c���タ(xi��n)C�й����c(di��n)�_��
�c���タ(xi��n)C�й����c(di��n)�_��![]()
ԇ�}�������� ��1������1����2������y2��2px���ã���2��2��2p��1��
����p��2��
������Ē��タ(xi��n)C�ķ��̞�![]()
���(zh��n)��(xi��n)���̞�![]() ��
��
��2�����O(sh��)���ڷ����}���ֱ��(xi��n)![]() ��
��
�䷽�̞�![]() ��
��
��![]() ��
��![]() ��
��
��?y��n)�ֱ��(xi��n)![]() �c���タ(xi��n)C�й����c(di��n)��
�c���タ(xi��n)C�й����c(di��n)��
��������4��8t��0�����![]() ��
��
��һ���棬��ֱ��(xi��n)OA��![]() �ľ��x
�ľ��x![]()
�ɵ�![]() �����
�����![]() ��
��
��?y��n)�?/span>1[��![]() ����������1��[��
����������1��[��![]() ����������
����������
���Է����}���ֱ��(xi��n)![]() ���ڣ��䷽�̞�
���ڣ��䷽�̞�![]() ��
��
���c(di��n)�����タ(xi��n)���̣�ֱ��(xi��n)�c���タ(xi��n)λ���P(gu��n)ϵ
�������c(di��n)�������タ(xi��n)�Ę�(bi��o)��(zh��n)���̵ķ���������
��1�����������タ(xi��n)�Ę�(bi��o)��(zh��n)���̳��ô���ϵ��(sh��)������?y��n)�δ֪�?sh��)ֻ��p������ֻ��һ��(g��)�l���_��pֵ���ɣ�
��2�����̣���?y��n)钁�タ(xi��n)�������ķN��(bi��o)��(zh��n)��ʽ��������タ(xi��n)���̕r(sh��)�����ȶ�λ���ٶ�����
���ѣ����(bi��o)��(zh��n)����Ҫ�ȴ_����ʽ����Ҫ�r(sh��)Ҫ�M(j��n)�з��(l��i)ӑՓ����(bi��o)��(zh��n)�����Еr(sh��)���O(sh��)��y2=mx��x2=my��m��0����
���}�͡�����}
���Y(ji��)����
22
���}Ŀ����֪�E�A![]() ��
��![]() �����ҽ��c(di��n)�c����S��һ��(g��)���c(di��n)���������ε�����(g��)��c(di��n)���c(di��n)
�����ҽ��c(di��n)�c����S��һ��(g��)���c(di��n)���������ε�����(g��)��c(di��n)���c(di��n)![]() �ڙE�A
�ڙE�A![]() ��.
��.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2��ֱ��(xi��n)![]() �^(gu��)�E�A���c(di��n)
�^(gu��)�E�A���c(di��n)![]() ���E�A��
���E�A��![]() ��
��![]() ��E�A���S������c(di��n)����(d��ng)ֱ��(xi��n)
��E�A���S������c(di��n)����(d��ng)ֱ��(xi��n)![]() �r(sh��)����
�r(sh��)����![]() ����e.
����e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������ABC�У���A��B��C��(du��)��(y��ng)��߅�քe��a��b��c����֪cos2A��3cos��B+C��=1��
��1�����A�Ĵ�С��
��2������ABC����eS=5![]() ��b=5����sinBsinC��ֵ��
��b=5����sinBsinC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��ӑՓ����(sh��)![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2����ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() �Ľ��c(di��n)�ęM����(bi��o)��
�Ľ��c(di��n)�ęM����(bi��o)��![]() ����
����![]() ��������(sh��)
��������(sh��)![]() ���п��ܵ�ֵ.
���п��ܵ�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
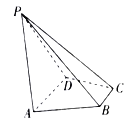
���}Ŀ��(2017�����K�߿�)��D���������FABCD�У�AB��AD��BC��BD��ƽ��ABD��ƽ��BCD���c(di��n)E��F(E�cA��D���غ�)�քe����AD��BD�ϣ���EF��AD.

���C��(1)EF��ƽ��ABC��
(2)AD��AC.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com