
【題目】如圖,在幾何體ABCDE中,四邊形ABCD是矩形,AB![]() 平面BEC,BE
平面BEC,BE![]() EC,AB=BE=EC=2,G,F分別是線段BE,DC的中點.
EC,AB=BE=EC=2,G,F分別是線段BE,DC的中點.
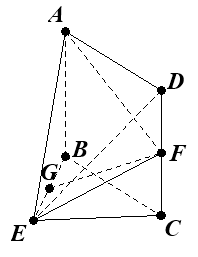
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求平面AEF與平面BEC所成銳二面角的余弦值.
【答案】(Ⅰ)詳見解析;(Ⅱ) ![]() .
.
【解析】解法一:(Ⅰ)如圖,取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,又G是BE的中點,
,又G是BE的中點,![]() ,
,
又F是CD中點,![]() ,由四邊形ABCD是矩形得,
,由四邊形ABCD是矩形得,![]() ,所以
,所以![]() .從而四邊形
.從而四邊形![]() 是平行四邊形,所以
是平行四邊形,所以![]() ,,又
,,又![]() ,所以
,所以![]() .
.
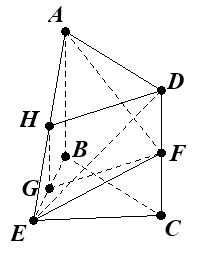

(Ⅱ)如圖,在平面BEC內,過點B作![]() ,因為
,因為![]() .
.
又因為AB![]() 平面BEC,所以AB
平面BEC,所以AB![]() BE,AB
BE,AB![]() BQ
BQ
以B為原點,分別以![]() 的方向為x軸,y軸,z軸的正方向建立空間直角坐標系,則A(0,0,2),B(0,0,0),E(2,0,0),F(2,2,1).因為AB
的方向為x軸,y軸,z軸的正方向建立空間直角坐標系,則A(0,0,2),B(0,0,0),E(2,0,0),F(2,2,1).因為AB![]() 平面BEC,所以
平面BEC,所以![]() 為平面BEC的法向量,
為平面BEC的法向量,
設![]() 為平面AEF的法向量.又
為平面AEF的法向量.又![]()
由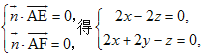 取
取![]() 得
得![]() .
.
從而![]()
所以平面AEF與平面BEC所成銳二面角的余弦值為![]() .
.
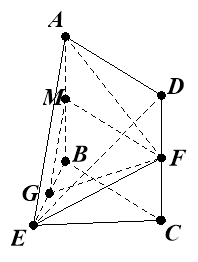
解法二:(Ⅰ)如圖,取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,又
,又![]() 是
是![]() 的中點,可知
的中點,可知![]() ,
,
又![]() 面
面![]() ,
,![]() 面
面![]() ,所以
,所以![]() 平面
平面![]() .
.
在矩形ABCD中,由M,F分別是AB,CD的中點得![]() .
.
又![]() 面
面![]() ,
,![]() 面
面![]() ,所以
,所以![]() 面
面![]() .
.
又因為![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,
所以面![]() 平面
平面![]() ,因為
,因為![]() 面
面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)同解法一.


科目:高中數學 來源: 題型:
【題目】為積極響應國家“陽光體育運動”的號召,某學校在了解到學生的實際運動情況后,發起以“走出教室,走到操場,走到陽光”為口號的課外活動倡議。為調查該校學生每周平均體育運動時間的情況,從高一高二基礎年級與高三三個年級學生中按照4:3:3的比例分層抽樣,收集300位學生每周平均體育運動時間的樣本數據(單位:小時),得到如圖所示的頻率分布直方圖。

(1)據圖估計該校學生每周平均體育運動時間.并估計高一年級每周平均體育運動時間不足4小時的人數;
(2)規定每周平均體育運動時間不少于6小時記為“優秀”,否則為“非優秀”,在樣本數據中,有30位高三學生的每周平均體育運動時間不少于6小時,請完成下列![]() 列聯表,并判斷是否有99%的把握認為“該校學生的每周平均體育運動時間是否“優秀”與年級有關”.
列聯表,并判斷是否有99%的把握認為“該校學生的每周平均體育運動時間是否“優秀”與年級有關”.
基礎年級 | 高三 | 合計 | |
優秀 | |||
非優秀 | |||
合計 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每年春晚都是萬眾矚目的時刻,這些節目體現的文化內涵、歷史背景等反映了社會的進步.國家的富強,人民生活水平的提高等.某學校高三年級主任開學初為了解學生在看春晚后對節目體現的文化內涵、歷史背景等是否會在今年的高考題中體現進行過思考,特地隨機抽取100名高三學生(其中文科學生50,理科學生50名),進行了調查.統計數據如表所示(不完整):
“思考過” | “沒有思考過” | 總計 | |
文科學生 | 40 | 10 | |
理科學生 | 30 | ||
總計 | 100 |
(1)補充完整所給表格,并根據表格數據計算是否有![]() 的把握認為看春晚后會思考節目體現的文化內涵、歷史背景等與文理科學生有關;
的把握認為看春晚后會思考節目體現的文化內涵、歷史背景等與文理科學生有關;
(2)①現從上表的”思考過”的文理科學生中按分層抽樣選出7人.再從這7人中隨機抽取4人,記這4人中“文科學生”的人數為![]() ,試求
,試求![]() 的分布列與數學期望;
的分布列與數學期望;
②現設計一份試卷(題目知識點來自春晚相關知識整合與變化),假設“思考過”的學生及格率為![]() ,“沒有思考過”的學生的及格率為
,“沒有思考過”的學生的及格率為![]() .現從“思考過”與“沒有思考過”的學生中分別隨機抽取一名學生進行測試,求兩人至少有一個及格的概率.
.現從“思考過”與“沒有思考過”的學生中分別隨機抽取一名學生進行測試,求兩人至少有一個及格的概率.
附參考公式: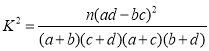 ,其中
,其中![]() .
.
參考數據:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業產值在2008年~2017年的年增量(即當年產值比前一年產值增加的量)統計圖如圖所示(單位:萬元),下列說法正確的是( )
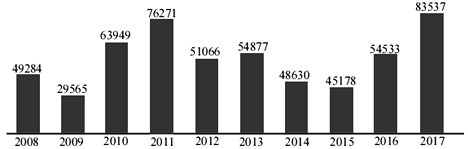
A. 2009年產值比2008年產值少
B. 從2011年到2015年,產值年增量逐年減少
C. 產值年增量的增量最大的是2017年
D. 2016年的產值年增長率可能比2012年的產值年增長率低
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有甲、乙兩個班級進行數學考試,按照大于等于85分為優秀,85分以下為非優秀統計成績,得到如下所示的列聯表:
優秀 | 非優秀 | 總計 | |
甲班 | 10 | b | |
乙班 | c | 30 | |
總計105 |
已知在全部105人中隨機抽取1人,成績優秀的概率為![]() ,則下列說法正確的是( )
,則下列說法正確的是( )
參考公式: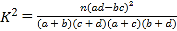
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
A.列聯表中c的值為30,b的值為35
B.列聯表中c的值為15,b的值為50
C.根據列聯表中的數據,若按95%的可靠性要求,能認為“成績與班級有關系”
D.根據列聯表中的數據,若按95%的可靠性要求,不能認為“成績與班級有關系”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某單位甲、乙、丙三個部門的員工人數分別為24,16,16.現采用分層抽樣的方法從中抽取7人,進行睡眠時間的調查.
(I)應從甲、乙、丙三個部門的員工中分別抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,現從這7人中隨機抽取3人做進一步的身體檢查.
(i)用X表示抽取的3人中睡眠不足的員工人數,求隨機變量X的分布列與數學期望;
(ii)設A為事件“抽取的3人中,既有睡眠充足的員工,也有睡眠不足的員工”,求事件A發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,底面
,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
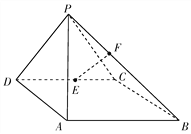
(Ⅰ)求證: ![]() ;
;
(Ⅱ)試確定點![]() 的位置,使得直線
的位置,使得直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等.
所成的角相等.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大提出,堅決打贏脫貧攻堅戰,某幫扶單位為幫助定點扶貧村真脫貧,堅持扶貧同扶智相結合,幫助貧困村種植蜜柚,并利用電商進行銷售,為了更好地銷售,現從該村的蜜柚樹上隨機摘下了100個蜜柚進行測重,其質量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 單位:克
單位:克![]() 中,其頻率分布直方圖如圖所示.
中,其頻率分布直方圖如圖所示.

![]() Ⅰ
Ⅰ![]() 按分層抽樣的方法從質量落在
按分層抽樣的方法從質量落在![]() ,
,![]() 的蜜柚中抽取5個,再從這5個蜜柚中隨機抽取2個,求這2個蜜柚質量均小于2000克的概率;
的蜜柚中抽取5個,再從這5個蜜柚中隨機抽取2個,求這2個蜜柚質量均小于2000克的概率;
![]() Ⅱ
Ⅱ![]() 以各組數據的中間數代表這組數據的平均水平,以頻率代表概率,已知該貧困村的蜜柚樹上大約還有5000個蜜柚等待出售,某電商提出兩種收購方案:
以各組數據的中間數代表這組數據的平均水平,以頻率代表概率,已知該貧困村的蜜柚樹上大約還有5000個蜜柚等待出售,某電商提出兩種收購方案:
A.所有蜜柚均以40元![]() 千克收購;
千克收購;
B.低于2250克的蜜柚以60元![]() 個收購,高于或等于2250克的以80元
個收購,高于或等于2250克的以80元![]() 個收購.
個收購.
請你通過計算為該村選擇收益最好的方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com