【題目】在三棱柱
中，
與
均為等邊三角形，
，O為BC的中點.
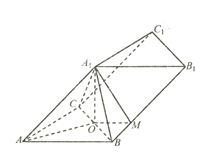
（1）證明：平面
平面ABC；
（2）在棱
上確定一點M，使得二面角
的大小為
.
【答案】（1）見解析（2）
【解析】
（1）要證明平面
平面ABC，只需證明
平面ABC即可．因為
為等邊三角形，所以
再根據勾股定理證明
，即可證出平面ABC；
（2）以OA，OB，
所在直線分別為x軸，y軸，z軸，建立如圖所示的空間直角坐標系O-xyz，根據向量共線定理用參數
表示出點
的坐標，分別求出平面
和平面
的法向量，由二面角的向量公式列式，即可求出參數，確定的位置．
（1）因為
與均為等邊三角形，
，O為BC的中點，
所以
.
在
中，
，
從而有
，所以，
又因為
，所以平面ABC，
又因為
平面
，所以平面平面ABC．
（2）以OA，OB，所在直線分別為x軸，y軸，z軸
建立如圖所示的空間直角坐標系O-xyz，
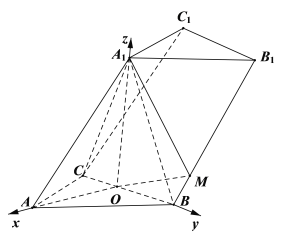
則
，
，由（1）可知，
平面，
是平面的一個法向量，
設
，其中
.
所以
，
，
設平面的法向量為
，
則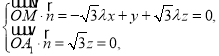
取
，則
，
所以
，
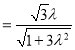
解得
.
即存在一點M，且時，二面角
的大小為
.
科目：高中數學 來源： 題型：
【題目】受轎車在保修期內維修費等因素的影響，企業生產每輛轎車的利潤與該轎車首次出現故障的時間有關．某轎車制造廠生產甲、乙兩種品牌轎車，保修期均為2年．現從該廠已售出的兩種品牌轎車中各隨機抽取50輛，統計數據如下：
品牌 | 甲 | 乙 | |||
首次出現故 障時間x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
轎車數量(輛) | 2 | 3 | 45 | 5 | 45 |
每輛利潤 (萬元) | 1 | 2 | 3 | 1.8 | 2.9 |
將頻率視為概率，解答下列問題：
(1)從該廠生產的甲品牌轎車中隨機抽取一輛，求其首次出現故障發生在保修期內的概率．
(2)若該廠生產的轎車均能售出，記生產一輛甲品牌轎車的利潤為X1，生產一輛乙品牌轎車的利潤為X2，分別求X1，X2的分布列．
(3)該廠預計今后這兩種品牌轎車銷量相當，由于資金限制，只能生產其中一種品牌的轎車．若從經濟效益的角度考慮，你認為應生產哪種品牌的轎車？說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知一個數列的各項是1和2，首項是1，且在第
個1和第
個1之間有
個2，即1，2，1，2，2，1，2，2，2，2，1，2，2，2，2，2，2，2，2，1…，則此數列的前2017項的和
______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知圓錐的頂點為S，底面圓O的兩條直徑分別為AB和CD，且AB⊥CD，若平面
平面
．現有以下四個結論：
①AD∥平面SBC；
②
；
③若E是底面圓周上的動點，則△SAE的最大面積等于△SAB的面積；
④
與平面SCD所成的角為45°．
其中正確結論的序號是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
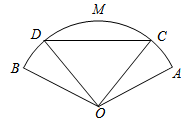
【題目】如圖，有一塊半徑為20米，圓心角
的扇形展示臺，展示臺分成了四個區域：三角形
，弓形
，扇形
和扇形
（其中
）.某次菊花展依次在這四個區域擺放：泥金香、紫龍臥雪、朱砂紅霜、朱砂紅霜.預計這三種菊花展示帶來的日效益分別是：泥金香50元/米
，紫龍臥雪30元/米，朱砂紅霜40元/米.
（1）設
，試建立日效益總量
關于
的函數關系式；
（2）試探求為何值時，日效益總量達到最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某班對一次實驗成績進行分析，利用隨機數表法抽取樣本時，先將50個同學按01，02．03，…50進行編號，然后從隨機數表第9行第11列的數開始向右讀，則選出的第6個個體是（ ）（注：表為隨機數表的第8行和第9行）
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
A.00B.13C.42D.44
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，設
為不同的兩點，直線
的方程為
，設
，其中
均為實數．下列四個說法中：
①存在實數
，使點
在直線上；
②若
，則過
兩點的直線與直線重合；
③若
，則直線經過線段
的中點；
④若
，則點在直線的同側，且直線與線段的延長線相交．
所有結論正確的說法的序號是______________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某運動員每次投籃命中的概率低于
，現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率：先由計算器產生0到9之間取整數值的隨機數，指定1，2，3，4表示命中，5，6，7，8，9，0表示不命中；再以每三個隨機數為一組，代表三次投籃的結果.經隨機模擬產生了如下20組隨機數：
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據此估計，該運動員三次投籃恰有兩次命中的概率為（ ）
A.0.35B.0.25C.0.20D.0.15
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
