
【題目】給出以下命題:
①雙曲線![]() 的漸近線方程為y=±
的漸近線方程為y=±![]() x;
x;
②命題p:“x∈R,sinx+![]() ≥2”是真命題;
≥2”是真命題;
③已知線性回歸方程為![]() =3+2x,當變量x增加2個單位,其預報值平均增加4個單位;
=3+2x,當變量x增加2個單位,其預報值平均增加4個單位;
④設隨機變量ξ服從正態分布N(0,1),若P(ξ>1)=0.2,則P(-1<ξ<0)=0.6;
⑤設![]() ,則
,則![]()
則正確命題的序號為________(寫出所有正確命題的序號).
科目:高中數學 來源: 題型:
【題目】寫出下列各隨機試驗的樣本空間:
(1)采用抽簽的方式,隨機選擇一名同學,并記錄其性別;
(2)采用抽簽的方式,隨機選擇一名同學,觀察其ABO血型;
(3)隨機選擇一個有兩個小孩的家庭,觀察兩個孩子的性別;
(4)射擊靶3次,觀察各次射擊中靶或脫靶情況;
(5)射擊靶3次,觀察中靶的次數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年某地初中畢業升學體育考試規定:考生必須參加長跑.擲實心球.1分鐘跳繩三項測試,三項測試各項20分,滿分60分.某學校在初三上學期開始時,為掌握全年級學生1分鐘跳繩情況,按照男女比例利用分層抽樣抽取了100名學生進行測試,其中女生54人,得到下面的頻率分布直方圖,計分規則如表1:
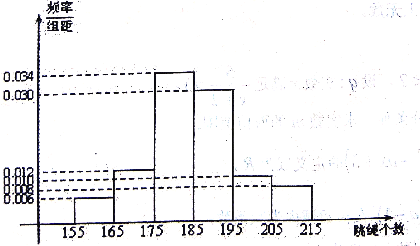

(1)規定:學生1分鐘跳繩得分20分為優秀,在抽取的100名學生中,男生跳繩個數大等于185個的有28人,根據已知條件完成表2,并根據這100名學生測試成績,能否有99%的把握認為學生1分鐘跳繩成績優秀與性別有關?
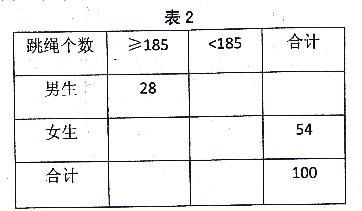
附:參考公式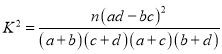
臨界值表:

(2)根據往年經驗,該校初三年級學生經過一年的訓練,正式測試時每人每分鐘跳繩個數都有明顯進步.假設今年正式測試時每人每分鐘跳繩個數比初三上學期開始時個數增加10個,全年級恰有2000名學生,所有學生的跳繩個數X服從正態分布N(μ,σ2)(用樣本數據的平值和方差估計總體的期望和方差,各組數據用中點值代替)
①估計正式測試時,1分鐘跳182個以上的人數(結果四舍五入到整數);
②若在全年級所有學生中任意選取3人,正式測試時1分鐘跳195個以上的人數為ξ,求ξ占的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產某種零件,每個零件的成本為40元,出廠單價定為60元,該廠為鼓勵銷售商訂購,決定當一次訂購量超過100個時,每多訂購一個,訂購的全部零件的出廠單價就降低0.02元,但實際出廠單價不能低于51元.
(1)當一次訂購量為多少個時,零件的實際出廠單價恰降為51元?
(2)設一次訂購量為![]() 個,零件的實際出廠單價為
個,零件的實際出廠單價為![]() 元.寫出函數
元.寫出函數![]() 的表達式;
的表達式;
(3)當銷售商一次訂購500個零件時,該廠獲得的利潤是多少元?如果訂購1000個,利潤又是多少元?(工廠售出一個零件的利潤=實際出廠單價-成本)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①函數![]() 的單調增區間是
的單調增區間是![]() ;
;
②若函數![]() 定義域為
定義域為![]() 且滿足
且滿足![]() ,則它的圖象關于
,則它的圖象關于![]() 軸對稱;
軸對稱;
③函數![]() 的值域為
的值域為![]() ;
;
④函數![]() 的圖象和直線
的圖象和直線![]() 的公共點個數是
的公共點個數是![]() ,則
,則![]() 的值可能是
的值可能是![]() ;
;
⑤若函數![]() 在
在![]() 上有零點,則實數
上有零點,則實數![]() 的取值范圍是
的取值范圍是![]() .
.
其中正確的序號是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,已知直線
軸的正半軸為極軸,建立極坐標系,已知直線![]() 的參數方程是
的參數方程是 (m>0,t為參數),曲線
(m>0,t為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與曲線
,與曲線![]() 交于點
交于點![]() ,且
,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了了解學生對電子競技的興趣,從該校高二年級的學生中隨機抽取了![]() 人進行檢查,已知這
人進行檢查,已知這![]() 人中有
人中有![]() 名男生對電子競技有興趣,而對電子競技沒興趣的學生人數與電子競技競技有興趣的女生人數一樣多,且女生中有
名男生對電子競技有興趣,而對電子競技沒興趣的學生人數與電子競技競技有興趣的女生人數一樣多,且女生中有![]() 的人對電子競技有興趣.
的人對電子競技有興趣.
![]() 在被抽取的女生中與
在被抽取的女生中與![]() 名高二
名高二![]() 班的學生,其中有
班的學生,其中有![]() 名女生對電子產品競技有興趣,先從這
名女生對電子產品競技有興趣,先從這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 人,求其中至少有
人,求其中至少有![]() 人對電子競技有興趣的概率;
人對電子競技有興趣的概率;
![]() 完成下面的
完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“電子競技的興趣與性別有關”.
的把握認為“電子競技的興趣與性別有關”.
有興趣 | 沒興趣 | 合計 | |
男生 | |||
女生 | |||
合計 |
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: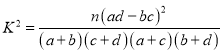
查看答案和解析>>
科目:高中數學 來源: 題型:
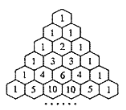
【題目】“楊輝三角”是我國數學史上的一個偉大成就,是二項式系數在三角形中的一種幾何排列.如圖所示,去除所有為1的項,依此構成數列2,3,3,4,6,4,5,10,10,5,…,則此數列的前46項和為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com