
【題目】定義集合![]() 與集合
與集合![]() 之差是由所有屬于
之差是由所有屬于![]() 且不屬于
且不屬于![]() 的元素組成的集合,記作
的元素組成的集合,記作![]() 且
且![]() .已知集合
.已知集合![]() .
.
(Ⅰ)若集合![]() ,寫出集合
,寫出集合![]() 的所有元素;
的所有元素;
(Ⅱ)從集合![]() 選出10個元素由小到大構成等差數列,其中公差的最大值
選出10個元素由小到大構成等差數列,其中公差的最大值![]() 和最小值
和最小值![]() 分別是多少?公差為
分別是多少?公差為![]() 和
和![]() 的等差數列各有多少個?
的等差數列各有多少個?
(Ⅲ)設集合![]() ,且集合
,且集合![]() 中含有10個元素,證明:集合
中含有10個元素,證明:集合![]() 中必有10個元素組成等差數列.
中必有10個元素組成等差數列.
【答案】(Ⅰ)2,4,8,16,32,64;(Ⅱ)![]() 只有1個,d=1有91個;(Ⅲ)見解析
只有1個,d=1有91個;(Ⅲ)見解析
【解析】
(Ⅰ)根據題意,分析集合T的元素,結合M﹣N的含義分析可得答案;(Ⅱ)根據題意,由等差數列的性質分析公差的最大、最小值,據此分析等差數列的數目,相加即可得答案;(Ⅲ)根據題意,將集合S中元素列表,據此分析集合集合S﹣A中的元素,由反證法分析可得結論.
(Ⅰ)根據題意,集合![]() ,
,![]()
![]() ;
;
則![]() ;
;
則集合![]() 的所有元素是: 2,4,8,16,32,64;
的所有元素是: 2,4,8,16,32,64;
(Ⅱ)當首項是1,末項是100時,公差最大為11,即![]() .
.
這樣的數列只有1個:1,12,23,34,45,56,67,78,89,100;
當選取的10個數是連續自然數時,公差最小為1,即d=1.
這樣的數列首項可以是1,2,3,…,91中的任何一個,
因此共有91個公差為1的等差數列;
(Ⅲ)將集合![]() 中元素列表如下:
中元素列表如下:
1 | 2 | 3 | … | 10 |
11 | 12 | 13 | … | 20 |
21 | 22 | 23 | … | 30 |
┆ | ┆ | ┆ | ┆ | ┆ |
91 | 92 | 93 | … | 100 |
表中各行或各列的十個數分別構成等差數列.
假設存在含有10個元素的集合![]() ,使得
,使得![]() 中不含10個元素組成的等差數列.
中不含10個元素組成的等差數列.
顯然每連續10個元素中必有集合中的唯一一個元素,即表的每行、每列中必有集合![]() 中的唯一一個元素.
中的唯一一個元素.
記表中第![]() 行第
行第![]() 列的數為
列的數為![]() .
.
若第![]() 行中集合A的唯一元素為
行中集合A的唯一元素為![]() ,則第
,則第![]() 行中
行中![]() ,
,![]() ,…
,…![]() 中必有集合A中元素.
中必有集合A中元素.
若第![]() 行的第一個數在集合
行的第一個數在集合![]() 中,則此行余下九個數和下一行第一個數可以組成等差數列,與假設矛盾.
中,則此行余下九個數和下一行第一個數可以組成等差數列,與假設矛盾.
因此,第一列中集合![]() 的唯一元素只可能在第十行.
的唯一元素只可能在第十行.
同理,若第![]() 行的第二個數在集合
行的第二個數在集合![]() 中,則此行余下八個數和下一行前兩個數可以組成等差數列,與假設矛盾.
中,則此行余下八個數和下一行前兩個數可以組成等差數列,與假設矛盾.
因此,第二列中集合![]() 的唯一元素只可能在第九行.
的唯一元素只可能在第九行.
依此類推,得![]() .
.
此時,另一條對角線上的十個元素![]() 構成等差數列,與假設矛盾.
構成等差數列,與假設矛盾.
綜上,原命題成立.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,右焦點為
,右焦點為![]() ,以原點
,以原點![]() 為圓心,橢圓
為圓心,橢圓![]() 的短半軸長為半徑的圓與直線
的短半軸長為半徑的圓與直線![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
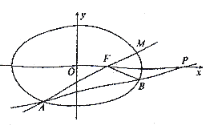
(2)如圖,過定點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,連接
兩點,連接![]() 并延長交
并延長交![]() 于
于![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用0,1,2,3,4,5這六個數字組成無重復數字的四位數.
(1)在組成的四位數中,求所有偶數的個數;
(2)在組成的四位數中,求比2430大的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的離心率
)的離心率![]() ,直線
,直線![]() 被以橢圓
被以橢圓![]() 的短軸為直徑的圓截得的弦長為
的短軸為直徑的圓截得的弦長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() ,
, ![]() 兩個不同的點,且
兩個不同的點,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將一枚質地均勻的硬幣向上拋擲三次,下列兩個事件中,是對立事件的是( )
A.事件![]() :“恰有兩次正面向上”,事件
:“恰有兩次正面向上”,事件![]() :“恰有兩次反面向上”
:“恰有兩次反面向上”
B.事件![]() :“恰有兩次正面向上”,事件
:“恰有兩次正面向上”,事件![]() :“恰有一次正面向上”
:“恰有一次正面向上”
C.事件![]() :“至少有一次正面向上”,事件
:“至少有一次正面向上”,事件![]() :“至多一次正面向上”
:“至多一次正面向上”
D.事件![]() :“至少有一次正面向上”,事件
:“至少有一次正面向上”,事件![]() :“恰有三次反面向上”
:“恰有三次反面向上”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓C:![]() (a>b>0)的左、右焦點分別為
(a>b>0)的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,過焦點
,過焦點![]() 且垂直于x軸的直線被橢圓C截得的線段長為1.
且垂直于x軸的直線被橢圓C截得的線段長為1.
(Ⅰ)求橢圓C的方程;
(Ⅱ)已知點M(0,-1),直線l經過點N(2,1)且與橢圓C相交于A,B兩點(異于點M),記直線MA的斜率為![]() ,直線MB的斜率為
,直線MB的斜率為![]() ,證明
,證明![]() 為定值,并求出該定值.
為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為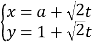 (
(![]() 為參數,
為參數, ![]() ),以
),以![]() 為極點,
為極點, ![]() 軸非負半軸為極軸,建立極坐標系,曲線
軸非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
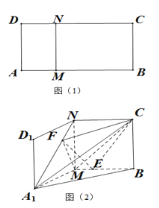
【題目】如圖1,矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 邊上異于端點的動點,
邊上異于端點的動點,![]() ,將矩形
,將矩形![]() 沿
沿![]() 折疊至
折疊至![]() 處,使面
處,使面![]() (如圖2).點
(如圖2).點![]() 滿足
滿足![]() ,
,![]() .
.
(1)證明:![]() ;
;
(2)設![]() ,當
,當![]() 為何值時,四面體
為何值時,四面體![]() 的體積最大,并求出最大值.
的體積最大,并求出最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com