
【題目】已知函數![]() 為偶函數,且在
為偶函數,且在![]() 上單調遞減,則
上單調遞減,則![]() 的解集為
的解集為![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線C1的參數方程為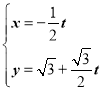 (t為參數),以O為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ2(1+sin2θ)=2,點M的極坐標為(
(t為參數),以O為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ2(1+sin2θ)=2,點M的極坐標為(![]() ,
,![]() ).
).
(1)求點M的直角坐標和C2的直角坐標方程;
(2)已知直線C1與曲線C2相交于A,B兩點,設線段AB的中點為N,求|MN|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個正方形花圃被分成5份.

(1)若給這5個部分種植花,要求相鄰兩部分種植不同顏色的花,己知現有紅、黃、藍、綠4種顏色不同的花,求有多少種不同的種植方法?
(2)若向這5個部分放入7個不同的盆栽,要求每個部分都有盆栽,問有多少種不同的放法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第一次大考后,某校對甲、乙兩個文科班的數學考試成績進行分析,規定:大于或等于![]() 分為優秀,
分為優秀,![]() 分以下為非優秀,統計成績后,得到如下
分以下為非優秀,統計成績后,得到如下![]() 列聯表,且已知在甲、乙兩個文科班全部
列聯表,且已知在甲、乙兩個文科班全部![]() 人中隨機抽取
人中隨機抽取![]() 人為優秀的概率為
人為優秀的概率為![]() .
.
(I)請完成![]() 列聯表:
列聯表:
優秀 | 非優秀 | 合計 | |
甲班 |
| ||
乙班 |
| ||
合計 |
|
(Ⅱ)根據列聯表的數據能否在犯錯誤的概率不超過![]() 的前提下認為成績與班級有關系?
的前提下認為成績與班級有關系?
參考公式和臨界值表:
 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業2018年招聘員工,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五種崗位的應聘人數、錄用人數和錄用比例(精確到1%)如下:
五種崗位的應聘人數、錄用人數和錄用比例(精確到1%)如下:
崗位 | 男性 應聘人數 | 男性 錄用人數 | 男性 錄用比例 | 女性 應聘人數 | 女性 錄用人數 | 女性 錄用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
總計 | 533 | 264 |
| 467 | 169 |
|
(1)從表中所有應聘人員中隨機選擇1人,試估計此人被錄用的概率;
(2)從應聘![]() 崗位的6人中隨機選擇2人.記
崗位的6人中隨機選擇2人.記![]() 為這2人中被錄用的人數,求
為這2人中被錄用的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 各崗位的男性、女性錄用比例都接近(二者之差的絕對值不大于
各崗位的男性、女性錄用比例都接近(二者之差的絕對值不大于![]() ),但男性的總錄用比例卻明顯高于女性的總錄用比例.研究發現,若只考慮其中某四種崗位,則男性、女性的總錄用比例也接近,請寫出這四種崗位.(只需寫出結論)
),但男性的總錄用比例卻明顯高于女性的總錄用比例.研究發現,若只考慮其中某四種崗位,則男性、女性的總錄用比例也接近,請寫出這四種崗位.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x2﹣2x﹣3≤0},B={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R}.
(1)若A∪B=A,求實數m的取值;
(2)若A∩B={x|0≤x≤3},求實數m的值;
(3)若A![]() ,求實數m的取值范圍.
,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的偶函數f(x)和奇函數g(x)滿足![]() .
.
(1)求函數f(x)和g(x)的表達式;
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍;
(3)若方程![]() 在
在![]() 上恰有一個實根,求實數m的取值范圍.
上恰有一個實根,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下給出了4個命題:
(1)兩個長度相等的向量一定相等;
(2)相等的向量起點必相同;
(3)若![]() ,且
,且![]() ,則
,則![]() ;
;
(4)若向量![]() 的模小于
的模小于![]() 的模,則
的模,則![]() .
.
其中正確命題的個數共有( )
A.3 個B.2 個C.1 個D.0個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com