
【題目】新高考改革后,國家只統(tǒng)一考試數(shù)學(xué)和語文,英語學(xué)科改為參加等級考試,每年考兩次,分別放在每個學(xué)年的上、下學(xué)期,物理、化學(xué)、生物、地理、歷史、政治這六科則以該省的省會考成績?yōu)闇?/span>.考生從中選擇三科成績,參加大學(xué)相關(guān)院系的錄取.
(1)若英語等級考試成績有一次為優(yōu),即可達到某211院校的錄取要求.假設(shè)某個學(xué)生參加每次等級考試事件是獨立的,且該生英語等級考試成績?yōu)閮?yōu)的概率都是![]() ,求該生在高二上學(xué)期的英語等級考試成績才為優(yōu)的概率;
,求該生在高二上學(xué)期的英語等級考試成績才為優(yōu)的概率;
(2)據(jù)預(yù)測,要想報考該211院校的相關(guān)院系,省會考的成績至少在90分以上,才有可能被該校錄取.假設(shè)該生在省會考六科的成績,考到90分以上概率都是![]() ,設(shè)該生在省會考時考到90分以上的科目數(shù)為
,設(shè)該生在省會考時考到90分以上的科目數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
【答案】(1) ![]() (2) 分布列見解析;數(shù)學(xué)期望2
(2) 分布列見解析;數(shù)學(xué)期望2
【解析】
(1)先用對立事件求得該生英語等級考試成績不為優(yōu)的概率為![]() ,再根據(jù)獨立事件的概率公式可得.
,再根據(jù)獨立事件的概率公式可得.
(2)利用二項分布的概率公式可得分布列,利用期望公式計算可得.
(1)記該生“英語等級考試成績?yōu)閮?yōu)”為事件![]() ,概率為
,概率為![]() ,則該生“英語等級考試成績不為優(yōu)”為事件
,則該生“英語等級考試成績不為優(yōu)”為事件![]() ,概率為
,概率為![]() ,則該生在高二上學(xué)期的英語等級考試成績才為優(yōu)的概率為
,則該生在高二上學(xué)期的英語等級考試成績才為優(yōu)的概率為 .
.
(2)解法一 由題意知![]() 的所有可能取值為0,1,2,3,4,5,6.
的所有可能取值為0,1,2,3,4,5,6.
則 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
所以隨機變量![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
|
![]() .
.
解法二 依題意得![]() ,
,
所以 ,
,![]() .
.
所以![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
|
![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某火鍋店為了解氣溫對營業(yè)額的影響,隨機記錄了該店1月份中5天的日營業(yè)額y(單位:千元)與該地當(dāng)日最低氣溫x(單位:℃)的數(shù)據(jù),如下表:
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
(1)求y關(guān)于x的回歸方程![]() ;
;
(2)判定y與x之間是正相關(guān)還是負相關(guān);若該地1月份某天的最低氣溫為6℃,用所求回歸方程預(yù)測該店當(dāng)日的營業(yè)額;
附:①![]() ;
; .
.
②參考數(shù)據(jù)如下:
i |
|
|
|
|
1 | 2 | 12 | 4 | 24 |
2 | 5 | 10 | 25 | 50 |
3 | 8 | 8 | 64 | 64 |
4 | 9 | 8 | 81 | 72 |
5 | 11 | 7 | 121 | 77 |
| 35 | 45 | 295 | 287 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,判斷函數(shù)
時,判斷函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)![]() 有兩個極值點時,求a的取值范圍,并證明
有兩個極值點時,求a的取值范圍,并證明![]() 的極大值大于2.
的極大值大于2.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線
為參數(shù)),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且設(shè)定點
兩點,且設(shè)定點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為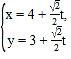 (
(![]() 為參數(shù)),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線
為參數(shù)),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且設(shè)定點
兩點,且設(shè)定點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出下列命題:
①線性相關(guān)系數(shù)![]() 越大,兩個變量的線性相關(guān)性越強;反之,線性相關(guān)性越弱;
越大,兩個變量的線性相關(guān)性越強;反之,線性相關(guān)性越弱;
②用![]() 來刻畫回歸效果,
來刻畫回歸效果,![]() 越大,說明模型的擬合效果越好;
越大,說明模型的擬合效果越好;
③根據(jù)![]() 列聯(lián)表中的數(shù)據(jù)計算得出的
列聯(lián)表中的數(shù)據(jù)計算得出的![]() 的值越大,兩類變量相關(guān)的可能性就越大;
的值越大,兩類變量相關(guān)的可能性就越大;
④在回歸分析模型中,殘差平方和越小,說明模型的擬合效果越好;
⑤從勻速傳遞的產(chǎn)品生產(chǎn)流水線上,質(zhì)檢員每10分鐘從中抽取一件產(chǎn)品進行某項指標檢測,這樣的抽樣是分層抽樣.
其中真命題的序號是_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)當(dāng)a>0時,求函數(shù)f(x)的單調(diào)區(qū)間;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)新研發(fā)了一種產(chǎn)品,產(chǎn)品的成本由原料成本及非原料成本組成,每件產(chǎn)品的非原料成本y(元)與生產(chǎn)該產(chǎn)品的數(shù)量x(千件)有關(guān),經(jīng)統(tǒng)計得到如下數(shù)據(jù):
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根據(jù)以上數(shù)據(jù),繪制了散點圖.
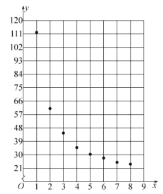
參考數(shù)據(jù):(其中![]() )
)
|
|
|
|
|
|
183.4 | 0.34 | 0.115 | 1.53 | 360 | 22385.8 |
參考公式:對于一組數(shù)據(jù)![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: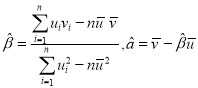 .
.
(1)觀察散點圖判斷,![]() 與
與![]() 哪一個適宜作為非原料成本y與生產(chǎn)該產(chǎn)品的數(shù)量x的回歸方程類型?(給出判斷即可,不必說明理由)
哪一個適宜作為非原料成本y與生產(chǎn)該產(chǎn)品的數(shù)量x的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(jù)(1)的判斷結(jié)果及表中數(shù)據(jù),建立y與x的回歸方程.
(3)試預(yù)測生產(chǎn)該產(chǎn)品10000件時每件產(chǎn)品的非原料成本.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com