
【題目】設數列{an}滿足a1=1,且an+1-an=n+1(n∈N*),則數列{an}的通項公式為________; ![]() 前10項的和為________.
前10項的和為________.
科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的兩條漸近線與拋物線
的兩條漸近線與拋物線![]() 的準線分別交于A,B兩點,O為坐標原點,若
的準線分別交于A,B兩點,O為坐標原點,若![]() ,則雙曲線的離心率
,則雙曲線的離心率![]() __________.
__________.
【答案】![]()
【解析】因為雙曲線![]() 的兩條漸近線為
的兩條漸近線為![]() ,拋物線
,拋物線![]() 的準線為
的準線為![]() ,所以
,所以![]() ,
,
因此![]()
點睛:解決橢圓和雙曲線的離心率的求值及范圍問題其關鍵就是確立一個關于![]() 的方程或不等式,再根據
的方程或不等式,再根據![]() 的關系消掉
的關系消掉![]() 得到
得到![]() 的關系式,而建立關于
的關系式,而建立關于![]() 的方程或不等式,要充分利用橢圓和雙曲線的幾何性質、點的坐標的范圍等.
的方程或不等式,要充分利用橢圓和雙曲線的幾何性質、點的坐標的范圍等.
【題型】填空題
【結束】
16
【題目】若函數![]() 滿足:對于
滿足:對于![]() 圖象上任意一點P,在其圖象上總存在點
圖象上任意一點P,在其圖象上總存在點![]() ,使得
,使得![]() 成立,稱函數
成立,稱函數![]() 是“特殊對點函數”.給出下列五個函數:
是“特殊對點函數”.給出下列五個函數:
①![]() ;②
;②![]() (其中e為自然對數的底數);③
(其中e為自然對數的底數);③![]() ;④
;④![]() ;
;
⑤![]() .
.
其中是“特殊對點函數”的序號是__________.(寫出所有正確的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 分別是橢圓C:
分別是橢圓C: ![]() 的左、右焦點,其中右焦點為拋物線
的左、右焦點,其中右焦點為拋物線![]() 的焦點,點
的焦點,點 在橢圓C上.
在橢圓C上.
(1)求橢圓C的標準方程;
(2)設與坐標軸不垂直的直線![]() 過
過![]() 與橢圓C交于A、B兩點,過點
與橢圓C交于A、B兩點,過點 且平行直線
且平行直線![]() 的直線交橢圓C于另一點N,若四邊形MNBA為平行四邊形,試問直線
的直線交橢圓C于另一點N,若四邊形MNBA為平行四邊形,試問直線![]() 是否存在?若存在,請求出
是否存在?若存在,請求出![]() 的斜率;若不存在,請說明理由.
的斜率;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠用7萬元錢購買了一臺新機器,運輸安裝費用2千元,每年投保、動力消耗的費用也為2千元,每年的保養、維修、更換易損零件的費用逐年增加,第一年為2千元,第二年為3千元,第三年為4千元,依此類推,即每年增加1千元.
(1)求使用n年后,保養、維修、更換易損零件的累計費用S(千元)關于n的表達式;
(2)問這臺機器最佳使用年限是多少年?并求出年平均費用(單位:千元)的最小值.(最佳使用年限是指使年平均費用最小的時間,年平均費用=(購入機器費用+運輸安裝費用+每年投保、動力消耗的費用+保養、維修、更換易損零件的累計費用)÷機器使用的年數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關命題的說法中錯誤的是( )
A. 設![]() ,則“
,則“![]() ”是“
”是“![]() ”的充要條件
”的充要條件
B. 若![]() 為真命題,則
為真命題,則![]() ,
, ![]() 中至少有一個為真命題
中至少有一個為真命題
C. 命題:“若![]() 是冪函數,則
是冪函數,則![]() 的圖象不經過第四象限”的否命題是假命題
的圖象不經過第四象限”的否命題是假命題
D. 命題“![]() ,
, ![]() 且
且![]() ”的否定形式是“
”的否定形式是“![]() ,
, ![]() 且
且![]() ”
”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】3月12日,全國政協總工會界別小組會議上,人社部副部長湯濤在回應委員呼聲時表示無論是從養老金方面,還是從人力資源的合理配置來說,延遲退休是大勢所趨.不過,湯部長也表示,不少職工對于延遲退休有著不同的意見.某高校一社團就是否同意延遲退休的情況隨機采訪了200名市民,并進行了統計,得到如下的![]() 列聯表:
列聯表:
贊同延遲退休 | 不贊同延遲退休 | 合計 | |
男性 | 80 | 20 | 100 |
女性 | 60 | 40 | 100 |
合計 | 140 | 60 | 200 |
(1)根據上面的列聯表判斷能否有![]() 的把握認為對延遲退休的態度與性別有關;
的把握認為對延遲退休的態度與性別有關;
(2)為了進一步征求對延遲退休的意見和建議,從抽取的200位市民中對不贊同的按照分層抽樣的方法抽取6人,再從這6人中隨機抽出3名進行電話回訪,求3人中至少有1人為男性的概率.
附: 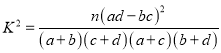 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某移動支付公司隨機抽取了100名移動支付用戶進行調查,得到如下數據:
每周移動支付次數 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合計 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)在每周使用移動支付超過3次的樣本中,按性別用分層抽樣隨機抽取5名用戶.
①求抽取的5名用戶中男、女用戶各多少人;
②從這5名用戶中隨機抽取2名用戶,求抽取的2名用戶均為男用戶的概率.
(2)如果認為每周使用移動支付次數超過3次的用戶“喜歡使用移動支付”,能否在犯錯誤概率不超過0.05的前提下,認為“喜歡使用移動支付”與性別有關?
附表及公式: 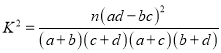
| 0.50 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 0.455 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com