【題目】設整數
是區間
中的不同整數.證明：集合
有這樣的子集存在，它的所有元素之和能被
整除.
【答案】見解析
【解析】
1.若
，則
個整數
都屬于
.于是，其中至少有二數相等，令
.
因，必有
.
于是
能被整除.
2.若
.不妨設
，考慮
個整數
，在其中任取三個數
.若
均能被
整除，則
，
從而，
，與
矛盾.
故
中至少有兩個數之差不能被整除.
不妨設
與
的差不能被整除，考慮個整數：
.
i. 若這個數關于模的余數都不同，則其中必有一個數能被整除，令此數為
.若
為偶數，結論成立；若為奇數，加上
即構成所需要的子集.
ii. 若這些數關于模有兩個以上的數同余，則任取其中二數之差必被整除，對照這些數的表達式知，因為和不同余，故二同余的數之差必為原集合中若干數之和.不妨仍記此和為，以下討論同i.
注：
是必要的，例如
時，結論對（0，6）的子集{1，3，4}不成立.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】定義在
上的函數
，如果滿足：對任意
，存在常數
，都有
成立，則稱
是
上的有界函數，其中
稱函數
的一個上界.已知函數
， 
.
（1）若函數
為奇函數，求實數
的值；
（2）在第（1）的條件下，求函數
在區間
上的所有上界構成的集合；
（3）若函數
在
上是以3為上界的有界函數，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】據氣象中心觀察和預測:發生于甲地的沙塵暴一直向正南方向移動，其移動速度
與時間
的函數圖象圖所示，過線段
上一點
作橫軸的垂線
，梯形
在直線左側部分的面積即為內沙塵暴所經過的路程
.
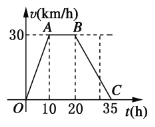
（1） 當
時，求
的值；
（2）將隨
變化的規律用數學關系式表示出來；
（3）若乙城位于甲地正南方向，且距甲地
，試判斷這場沙塵暴是否會侵襲到乙城，如果會，在沙塵暴發生后多長時間它將侵襲到乙城?如果不會，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列命題:
①非零向量
滿足
，則
和
的夾角為30°；
②將函數
的圖像按向量
平移，得到函數
的圖像；
③在三角形ABC中，若
，則三角形ABC為等腰三角形；其中正確命題的個數是（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
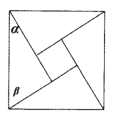
【題目】《周髀算經》中給出了弦圖，所謂弦圖是由四個全等的直角三角形和中間一個小正方形拼成一個大的正方形，若圖中直角三角形兩銳角分別為
，
，且小正方形與大正方形面積之比為
，則
的值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，以坐標原點為極點，
軸的正半軸為極軸建立極坐標系，已知曲線
的極坐標方程為
，過點
的直線
的參數方程為
（
為參數），直線與曲線相交于
，
兩點.
（1）寫出曲線的直角坐標方程和直線的普通方程；
（2）若
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知傾斜角為
的直線
過點
和點
，點在第一象限，
.
（1）求的坐標；
（2）若直線與兩平行直線
，
相交于
、
兩點，且
，求實數
的值；
（3）記集合
直線
經過點且與坐標軸圍成的面積為
，
，針對
的不同取值，討論集合
中的元素個數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
