
【題目】設(shè)函數(shù)![]() 的定義域為
的定義域為![]() ,如果存在非零常數(shù)
,如果存在非零常數(shù)![]() ,對于任意
,對于任意![]() ,都有
,都有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 是“似周期函數(shù)”,非零常數(shù)
是“似周期函數(shù)”,非零常數(shù)![]() 為函數(shù)
為函數(shù)![]() 的“似周期”.現(xiàn)有下面四個關(guān)于“似周期函數(shù)”的命題:
的“似周期”.現(xiàn)有下面四個關(guān)于“似周期函數(shù)”的命題:
①如果“似周期函數(shù)”![]() 的“似周期”為-1,那么它是周期為2的周期函數(shù);
的“似周期”為-1,那么它是周期為2的周期函數(shù);
②函數(shù)![]() 是“似周期函數(shù)”;
是“似周期函數(shù)”;
③函數(shù)![]() 是“似周期函數(shù)”;
是“似周期函數(shù)”;
④如果函數(shù)![]() 是“似周期函數(shù)”,那么“
是“似周期函數(shù)”,那么“![]() ”.
”.
其中是真命題的序號是 .(寫出所有滿足條件的命題序號)
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=丨x+a+1丨+丨x-![]() 丨,(a>0)。
丨,(a>0)。
(1)證明:f(x)≥5;
(2)若f(1)<6成立,求實數(shù)a的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
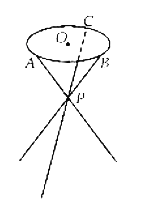
【題目】如圖,小凳凳面為圓形,凳腳為三根細鋼管.考慮到鋼管的受力等因素,設(shè)計的小凳應(yīng)滿足:三根細鋼管相交處的節(jié)點![]() 與凳面圓形的圓心
與凳面圓形的圓心![]() 的連線垂直于凳面和地面,且
的連線垂直于凳面和地面,且![]() 分細鋼管上下兩段的比值為
分細鋼管上下兩段的比值為![]() ,三只凳腳與地面所成的角均為
,三只凳腳與地面所成的角均為![]() .若
.若![]() 、
、![]() 、
、![]() 是凳面圓周的三等分點,
是凳面圓周的三等分點,![]() 厘米,求凳子的高度
厘米,求凳子的高度![]() 及三根細鋼管的總長度(精確到
及三根細鋼管的總長度(精確到![]() ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
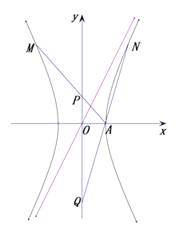
【題目】已知直線![]() 是雙曲線
是雙曲線![]() 的一條漸近線,點
的一條漸近線,點![]()
![]() 都在雙曲線
都在雙曲線![]() 上,直線
上,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,設(shè)坐標原點為
,設(shè)坐標原點為![]() .
.
(1)求雙曲線![]() 的方程,并求出點
的方程,并求出點![]() 的坐標(用
的坐標(用![]() 表示);
表示);
(2)設(shè)點![]() 關(guān)于
關(guān)于![]() 軸的對稱點為
軸的對稱點為![]() ,直線
,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() .問:在
.問:在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(3)若過點![]() 的直線
的直線![]() 與雙曲線
與雙曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,試求直線
,試求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
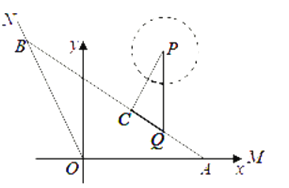
【題目】如圖,A、B是海岸線OM、ON上兩個碼頭,海中小島有碼頭Q到海岸線OM、ON的距離分別為![]() 、
、![]() ,測得
,測得![]() ,
,![]() ,以點O為坐標原點,射線OM為x軸的正半軸,建立如圖所示的直角坐標系,一艘游輪以
,以點O為坐標原點,射線OM為x軸的正半軸,建立如圖所示的直角坐標系,一艘游輪以![]() 小時的平均速度在水上旅游線AB航行(將航線AB看作直線,碼頭Q在第一象限,航線BB經(jīng)過點Q).
小時的平均速度在水上旅游線AB航行(將航線AB看作直線,碼頭Q在第一象限,航線BB經(jīng)過點Q).
(1)問游輪自碼頭A沿![]() 方向開往碼頭B共需多少分鐘?
方向開往碼頭B共需多少分鐘?
(2)海中有一處景點P(設(shè)點P在![]() 平面內(nèi),
平面內(nèi),![]() ,且
,且![]() ),游輪無法靠近,求游輪在水上旅游線AB航行時離景點P最近的點C的坐標.
),游輪無法靠近,求游輪在水上旅游線AB航行時離景點P最近的點C的坐標.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() x∈R,其中a,b∈R.
x∈R,其中a,b∈R.
(Ⅰ)求f(x)的單調(diào)區(qū)間;
(Ⅱ)若f(x)存在極值點x0,且f(x1)= f(x0),其中x1≠x0,求證:x1+2x0=3;
(Ⅲ)設(shè)a>0,函數(shù)g(x)= |f(x)|,求證:g(x)在區(qū)間[0,2]上的最大值不小于![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四邊形ABCD為矩形,AB=2AD=4,M為AB的中點,將△ADM沿DM折起,得到四棱錐A1﹣DMBC,設(shè)A1C的中點為N,在翻折過程中,得到如下有三個命題:①BN∥平面A1DM;②三棱錐N﹣DMC的最大體積為![]() ;③在翻折過程中,存在某個位置,使得DM⊥A1C.其中正確命題的序號為_____.
;③在翻折過程中,存在某個位置,使得DM⊥A1C.其中正確命題的序號為_____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在極坐標系中,已知曲線![]() 的方程為
的方程為![]() ,曲線
,曲線![]() 的方程為
的方程為![]() .以極點
.以極點![]() 為原點,極軸為
為原點,極軸為![]() 軸正半軸建立直角坐標系
軸正半軸建立直角坐標系![]() .
.
(1)求曲線![]() ,
,![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,與曲線
,與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com