
【題目】在如圖所示的多面體中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC.BC=2AD=4,EF=3,AE=BE=2,G為BC的中點. 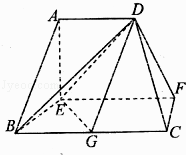
(1)求證:AB∥平面DEG;
(2)求證:BD⊥EG;
(3)求二面角C﹣DF﹣E的正弦值.
【答案】
(1)證明:∵AD∥EF,EF∥BC,∴AD∥BC,
∵BC=2AD,G為BC的中點,∴AD∥BG,且AD=BG,∴四邊形ABCD是平行四邊形,∴AB∥DG
因為AB不在平面DEG中,DG在平面DEG內,∴AB∥平面DEG
(2)證明:∵EF⊥平面AEB,AE平面AEB,BE平面AEB,
∴EF⊥AE,EF⊥BE,∵AE⊥EB,∴EB、EF、EA兩兩垂直.
以點E為坐標原點,EB、EF、EA所在直線分別為x、y、z軸建立空間直角坐標系,
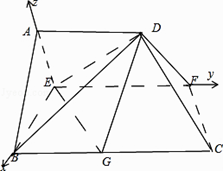
由已知得:A(0,0,2),B(2,0,0),C(2,4,0),D(0,2,2),F(0,3,0),G(2,2,0).
∵ ![]() ,∴
,∴ ![]()
∴BD⊥EG.
(3)解:由已知得 ![]() 是平面EFDA的法向量,設平面DCF的法向量為
是平面EFDA的法向量,設平面DCF的法向量為 ![]()
∵ ![]() ,∴
,∴ ![]() ,令z=1,得x=﹣1,y=2,即
,令z=1,得x=﹣1,y=2,即 ![]() .
.
設二面角C﹣DF﹣E的大小為θ,
則 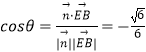 ,∴
,∴ ![]()
∴二面角C﹣DF﹣E的正弦值為 ![]() .
.
【解析】(1)要證AB∥平面DEG,可在平面DEG中找到一條直線與AB平行,根據題目給出的條件,能夠證得AB∥DG;(2)根據題目條件先證明EB、EA、EF兩兩相互垂直,然后以E為原點,以EB、EF、EA所在直線分別為x、y、z軸建立空間直角坐標系,運用向量數量積等于0 ![]() ,從而證明BD⊥EG;(3)在(2)的基礎上,求出二面角的兩個半平面的法向量,利用法向量求二面角的平面角的余弦值.
,從而證明BD⊥EG;(3)在(2)的基礎上,求出二面角的兩個半平面的法向量,利用法向量求二面角的平面角的余弦值.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】如圖,三棱錐A﹣BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4 ![]() ,CD=4
,CD=4 ![]() ,∠ACB=45°,E,F分別為MN的中點.
,∠ACB=45°,E,F分別為MN的中點. 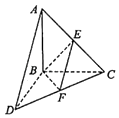
(1)求證:EF∥平面ABD;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:實數x滿足x2﹣4ax+3a2<0,其中a>0,命題q:實數x滿足 ![]() . (Ⅰ)若a=1,且p∧q為真,求實數x的取值范圍;
. (Ⅰ)若a=1,且p∧q為真,求實數x的取值范圍;
(Ⅱ)若¬p是¬q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知直線2x﹣y﹣4=0與直線x﹣2y+1=0交于點p.
(1)求過點p且垂直于直線3x+4y﹣15=0的直線l1的方程;(結果寫成直線方程的一般式)
(2)求過點P并且在兩坐標軸上截距相等的直線l2方程(結果寫成直線方程的一般式)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心為C的圓經過O(0,0))和A(4,0)兩點,線段OA的垂直平分線和圓C交于M,N兩點,且|MN|=2 ![]()
(1)求圓C的方程
(2)設點P在圓C上,試問使△POA的面積等于2的點P共有幾個?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于實數x的不等式﹣x2+bx+c<0的解集是{x|x<﹣3或x>2},則關于x的不等式cx2﹣bx﹣1>0的解集是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣2,3)
C.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.(﹣∞,﹣2)∪(3,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比數列,公比不為1.
(1)求數列{an}的通項公式;
(2)設bn= ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網店經營的一種商品進價是每件10元,根據一周的銷售數據得出周銷量P(件)與單價x(元)之間的關系如圖折線所示,該網店與這種商品有關的周開支均為25元.
(I)根據周銷量圖寫出周銷量P(件)與單價x(元)之間的函數關系式;
(Ⅱ)寫出周利潤y(元)與單價x(元)之間的函數關系式;當該商品的銷售價格為多少元時,周利潤最大?并求出最大周利潤.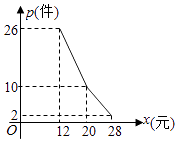
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com