
已知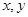 都是正數(shù),
都是正數(shù),
(1)若 ,求
,求 的最大值
的最大值
(2)若 ,求
,求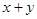 的最小值.
的最小值.
(1)6;(2)36.
解析試題分析:(1)直接利用基本不等式 ,
,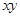 的最大值隨之而定;(2)如果直接利用基本不等式則有
的最大值隨之而定;(2)如果直接利用基本不等式則有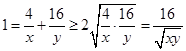 ①,
①,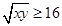 ,因此
,因此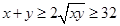 ②,這樣就可能得出
②,這樣就可能得出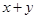 的最小值為32,實(shí)際上這個最小值是取不到的,因?yàn)椴坏仁舰偃〉忍柕臈l件是
的最小值為32,實(shí)際上這個最小值是取不到的,因?yàn)椴坏仁舰偃〉忍柕臈l件是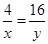 ,
,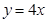 ,不等式②取等號的條件是
,不等式②取等號的條件是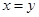 ,即不等式①②不能同時取等號,故
,即不等式①②不能同時取等號,故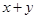 的最小值不是32.正確的解法是把
的最小值不是32.正確的解法是把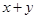 看作
看作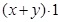 ,把其中的1用已知
,把其中的1用已知 代換,即
代換,即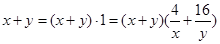 ,展開后就可以直接利用基本不等式求出結(jié)果.
,展開后就可以直接利用基本不等式求出結(jié)果.
試題解析:(1)xy=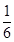 ·3x·2y≤
·3x·2y≤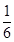
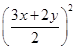 2=6 4分
2=6 4分
當(dāng)且僅當(dāng) 即
即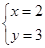 時取“=”號.
時取“=”號.
所以當(dāng)x=2,y=3時,xy取得最大值6 ..6分
(2)由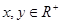 且
且 得
得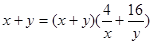
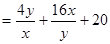
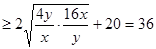 , 10分
, 10分
當(dāng)且僅當(dāng)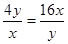 ,即x=12且y=24時,等號成立,
,即x=12且y=24時,等號成立,
所以x+y的最小值是36 12分
考點(diǎn):基本不等式的應(yīng)用.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知焦點(diǎn)在y軸,頂點(diǎn)在原點(diǎn)的拋物線C1經(jīng)過點(diǎn)P(2,2),以C1上一點(diǎn)C2為圓心的圓過定點(diǎn)A(0,1),記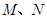 為圓
為圓 與
與 軸的兩個交點(diǎn).
軸的兩個交點(diǎn).
(1)求拋物線 的方程;
的方程;
(2)當(dāng)圓心 在拋物線上運(yùn)動時,試判斷
在拋物線上運(yùn)動時,試判斷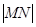 是否為一定值?請證明你的結(jié)論;
是否為一定值?請證明你的結(jié)論;
(3)當(dāng)圓心 在拋物線上運(yùn)動時,記
在拋物線上運(yùn)動時,記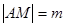 ,
, ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)f(x)=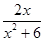 .
.
(1)若f(x)>k的解集為{x|x<-3,或x>-2},求k的值;
(2)對任意x>0,f(x)≤t恒成立,求t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,某小區(qū)擬在空地上建一個占地面積為2400平方米的矩形休閑廣場,按照設(shè)計(jì)要求,休閑廣場中間有兩個完全相同的矩形綠化區(qū)域,周邊及綠化區(qū)域之間是道路(圖中陰影部分),道路的寬度均為2米.怎樣設(shè)計(jì)矩形休閑廣場的長和寬,才能使綠化區(qū)域的總面積最大?并求出其最大面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
交通管理部門為了優(yōu)化某路段的交通狀況,經(jīng)過對該路段的長期觀測發(fā)現(xiàn):在交通繁忙的時段內(nèi),該路段內(nèi)汽車的車流量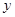 (千輛/時)與汽車的平均速度
(千輛/時)與汽車的平均速度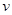 (千米/時)之間的函數(shù)關(guān)系為
(千米/時)之間的函數(shù)關(guān)系為
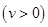
①求在該路段內(nèi),當(dāng)汽車的平均速度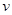 為多少時,車流量最大?最大車流量為多少?(精確到
為多少時,車流量最大?最大車流量為多少?(精確到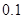 千輛/時)
千輛/時)
②若要求在該時段內(nèi)車流量超過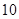 千輛/時,則汽車的平均速度應(yīng)限定在什么范圍內(nèi)?
千輛/時,則汽車的平均速度應(yīng)限定在什么范圍內(nèi)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知不等式2|x-3|+|x-4|<2a.
(Ⅰ)若a=1,求不等式的解集;
(Ⅱ)若已知不等式的解集不是空集,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
已知圓C過點(diǎn)(1,0),且圓心在x軸的正半軸上,直線l: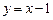 被該圓所截得
被該圓所截得
的弦長為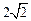 ,則圓
,則圓 C的標(biāo)準(zhǔn)方程為 .
C的標(biāo)準(zhǔn)方程為 .
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com