
【題目】某連鎖經(jīng)營公司所屬5個(gè)零售店某月的銷售額和利潤額如下表:
商店名稱 | A | B | C | D | E |
銷售額x/千萬元 | 3 | 5 | 6 | 7 | 9 |
利潤額y/百萬元 | 2 | 3 | 3 | 4 | 5 |
(1)畫出散點(diǎn)圖,觀察散點(diǎn)圖,說明兩個(gè)變量是否線性相關(guān);
(2)用最小二乘法計(jì)算利潤額y對銷售額x的線性回歸方程;
(3)當(dāng)銷售額為4千萬元時(shí),估計(jì)利潤額的大小.
(參考公式: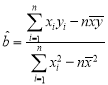 ,
,![]() )
)
【答案】(1)圖見解析,變量![]() 線性相關(guān);(2)
線性相關(guān);(2)![]() ;(3)2.4百萬元
;(3)2.4百萬元
【解析】
(1)根據(jù)題中數(shù)據(jù)在直角坐標(biāo)系中作出這五個(gè)點(diǎn),即可得到散點(diǎn)圖,并由圖觀察這些點(diǎn)是否在一條直線附近,即可判斷;
(2)根據(jù)公式分別求出![]() ,即可求出;
,即可求出;
(3)由(2)中求出的回歸方程,將![]() 代入,即可估計(jì)利潤額的大小.
代入,即可估計(jì)利潤額的大小.
解:(1)散點(diǎn)圖如圖所示.
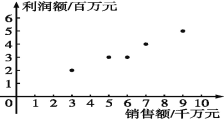
由散點(diǎn)圖可以看出變量![]() 線性相關(guān).
線性相關(guān).
(2)設(shè)線性回歸方程是![]() .
.
因?yàn)?/span>![]() ,所以
,所以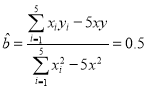 ,
,
![]() ,
,
即利潤額y對銷售額x的線性回歸方程為![]() .
.
(3)當(dāng)銷售額為4千萬元時(shí),利潤額約為![]() (百萬元).
(百萬元).


 本土教輔贏在暑假高效假期總復(fù)習(xí)云南科技出版社系列答案
本土教輔贏在暑假高效假期總復(fù)習(xí)云南科技出版社系列答案 暑假作業(yè)北京藝術(shù)與科學(xué)電子出版社系列答案
暑假作業(yè)北京藝術(shù)與科學(xué)電子出版社系列答案 第三學(xué)期贏在暑假系列答案
第三學(xué)期贏在暑假系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)命題p:x0∈(1,+∞),使得5+|x0|=6.q:x∈(0,+∞),![]() +81x≥a.
+81x≥a.
(1)若a=9,判斷命題¬p,p∨q,(¬p)∧(¬q)的真假,并說明理由;
(2)設(shè)命題r:x0∈R,x02+2x0+a-9≤0判斷r成立是q成立的什么條件,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方體![]() 中,
中,![]() ,
,![]() 分別是棱
分別是棱![]() ,
,![]() 的中點(diǎn),
的中點(diǎn),![]() 為棱
為棱![]() 上一點(diǎn),
上一點(diǎn),![]() 且
且![]() 平面
平面![]() .
.
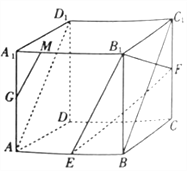
(1)證明:![]() 為
為![]() 中點(diǎn);
中點(diǎn);
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某兒童樂園在“六一”兒童節(jié)推出了一項(xiàng)趣味活動(dòng).參加活動(dòng)的兒童需轉(zhuǎn)動(dòng)如圖所示的轉(zhuǎn)盤兩次,每次轉(zhuǎn)動(dòng)后,待轉(zhuǎn)盤停止轉(zhuǎn)動(dòng)時(shí),記錄指針?biāo)竻^(qū)域中的數(shù).設(shè)兩次記錄的數(shù)分別為x,y.獎(jiǎng)勵(lì)規(guī)則如下:

①若![]() ,則獎(jiǎng)勵(lì)玩具一個(gè);
,則獎(jiǎng)勵(lì)玩具一個(gè);
②若![]() ,則獎(jiǎng)勵(lì)水杯一個(gè);
,則獎(jiǎng)勵(lì)水杯一個(gè);
③其余情況獎(jiǎng)勵(lì)飲料一瓶.
假設(shè)轉(zhuǎn)盤質(zhì)地均勻,四個(gè)區(qū)域劃分均勻.小亮準(zhǔn)備參加此項(xiàng)活動(dòng).
(Ⅰ)求小亮獲得玩具的概率;
(Ⅱ)請比較小亮獲得水杯與獲得飲料的概率的大小,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的中心在原點(diǎn),焦點(diǎn)在
的中心在原點(diǎn),焦點(diǎn)在![]() 軸,離心率為
軸,離心率為![]() ,且長軸長是短軸長的
,且長軸長是短軸長的![]() 倍.
倍.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)![]() 過橢圓
過橢圓![]() 左焦點(diǎn)
左焦點(diǎn)![]() 的直線
的直線![]() 交
交![]() 于
于![]() ,
, ![]() 兩點(diǎn),若對滿足條件的任意直線
兩點(diǎn),若對滿足條件的任意直線![]() ,不等式
,不等式![]()
![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖是2018年第一季度五省GDP情況圖,則下列描述中不正確的是( )
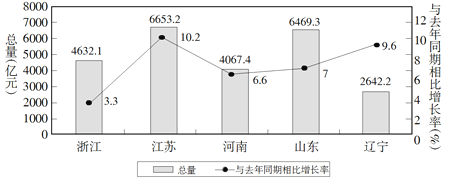
A. 與去年同期相比2018年第一季度五個(gè)省的GDP總量均實(shí)現(xiàn)了增長
B. 2018年第一季度GDP增速由高到低排位第5的是浙江省
C. 2018年第一季度GDP總量和增速由高到低排位均居同一位的省只有1個(gè)
D. 去年同期河南省的GDP總量不超過4000億元
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形![]() 中,
中, ![]() ,
, ![]() 與
與![]() 交于
交于![]() 點(diǎn),現(xiàn)將
點(diǎn),現(xiàn)將![]() 沿
沿![]() 折起得到三棱錐
折起得到三棱錐![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點(diǎn).
的中點(diǎn).
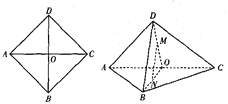
(1)求證: ![]() ;
;
(2)若三棱錐![]() 的最大體積為
的最大體積為![]() ,當(dāng)三棱錐
,當(dāng)三棱錐![]() 的體積為
的體積為![]() ,且二面角
,且二面角![]() 為銳角時(shí),求二面角
為銳角時(shí),求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線![]() 右支上的一點(diǎn)
右支上的一點(diǎn)![]() ,經(jīng)過點(diǎn)
,經(jīng)過點(diǎn)![]() 的直線與雙曲線
的直線與雙曲線![]() 的兩條漸近線分別相交于
的兩條漸近線分別相交于![]() ,
,![]() 兩點(diǎn).若點(diǎn)
兩點(diǎn).若點(diǎn)![]() ,
,![]() 分別位于第一,四象限,
分別位于第一,四象限,![]() 為坐標(biāo)原點(diǎn).當(dāng)
為坐標(biāo)原點(diǎn).當(dāng)![]() 時(shí),
時(shí),![]() 為( )
為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 與
與![]() 均為等邊三角形,點(diǎn)
均為等邊三角形,點(diǎn)![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).

(1)證明:平面![]() 平面
平面![]() ;
;
(2)試問在線段![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使二面角
,使二面角![]() 的余弦值為
的余弦值為![]() ,若存在,請確定點(diǎn)
,若存在,請確定點(diǎn)![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com