
【題目】隨著經(jīng)濟(jì)的不斷發(fā)展和人們消費(fèi)觀念的不斷提升,越來(lái)越多的人日益喜愛(ài)旅游觀光.某人想在2019年5月到某景區(qū)![]() 旅游觀光,為了避開(kāi)旅游高峰擁擠,方便出行,他收集了最近5個(gè)月該景區(qū)的觀光人數(shù)數(shù)據(jù)見(jiàn)下表:
旅游觀光,為了避開(kāi)旅游高峰擁擠,方便出行,他收集了最近5個(gè)月該景區(qū)的觀光人數(shù)數(shù)據(jù)見(jiàn)下表:
月份 | 2018.12 | 2019.1 | 2019.2 | 2019.3 | 2019.4 |
月份編號(hào) | 1 | 2 | 3 | 4 | 5 |
旅游觀光人數(shù) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)由收集數(shù)據(jù)的散點(diǎn)圖發(fā)現(xiàn),可用線性回歸模型擬合旅游觀光人數(shù)少![]() (百萬(wàn)人)與月份編號(hào)
(百萬(wàn)人)與月份編號(hào)![]() 之間的相關(guān)關(guān)系,請(qǐng)用最小二乘法求
之間的相關(guān)關(guān)系,請(qǐng)用最小二乘法求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ,并預(yù)測(cè)2019年5月景區(qū)
,并預(yù)測(cè)2019年5月景區(qū)![]() 的旅游觀光人數(shù).
的旅游觀光人數(shù).
(2)當(dāng)?shù)芈糜尉譃榱祟A(yù)測(cè)景區(qū)![]() 給當(dāng)?shù)氐呢?cái)政帶來(lái)的收入狀況,從2019年4月的旅游觀光人群中隨機(jī)抽取了200人,并對(duì)他們旅游觀光過(guò)程中的開(kāi)支情況進(jìn)行了調(diào)查,得到如下頻率分布表:
給當(dāng)?shù)氐呢?cái)政帶來(lái)的收入狀況,從2019年4月的旅游觀光人群中隨機(jī)抽取了200人,并對(duì)他們旅游觀光過(guò)程中的開(kāi)支情況進(jìn)行了調(diào)查,得到如下頻率分布表:
開(kāi)支金額(千元) |
|
|
|
|
|
|
|
頻數(shù) | 10 | 30 | 40 | 60 | 30 | 20 | 10 |
若采用分層抽樣的方法從開(kāi)支金額低于4千元的游客中抽取8人,再在這8人中抽取3人,記這3人中開(kāi)支金額低于3千元的人數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
(參考公式:![]() ,其中
,其中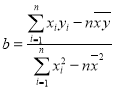 ,
,![]() .)
.)
【答案】(1)![]() ,2百萬(wàn)人;(2)分布列見(jiàn)解析,數(shù)學(xué)期望為
,2百萬(wàn)人;(2)分布列見(jiàn)解析,數(shù)學(xué)期望為![]() .
.
【解析】
(1)根據(jù)數(shù)據(jù)分別求得![]() ,
,![]() ,
,![]() ,
,![]() ,代入
,代入 ,求得b,
,求得b,![]() ,寫(xiě)出
,寫(xiě)出![]() 關(guān)于
關(guān)于![]() 的回歸方程,再令
的回歸方程,再令![]() 預(yù)測(cè)即可.
預(yù)測(cè)即可.
(2)根據(jù)分層抽樣,開(kāi)支金額為![]() ,
,![]() ,
,![]() (單位:千元)應(yīng)抽取的人數(shù)分別為1,3,4,則
(單位:千元)應(yīng)抽取的人數(shù)分別為1,3,4,則![]() ,1,2,3,分別求得相應(yīng)的概率,列出分布列再求期望.
,1,2,3,分別求得相應(yīng)的概率,列出分布列再求期望.
(1)![]() ,
,![]() ,
,
![]() ,
,![]() ,
, ,
,
所以![]() ,
,
所以![]() 關(guān)于
關(guān)于![]() 的回歸方程為
的回歸方程為![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() ,即預(yù)計(jì)2019年5月景區(qū)
,即預(yù)計(jì)2019年5月景區(qū)![]() 的旅游觀光人數(shù)為2百萬(wàn)人.
的旅游觀光人數(shù)為2百萬(wàn)人.
(2)由題意知開(kāi)支金額為![]() ,
,![]() ,
,![]() (單位:千元)應(yīng)抽取的人數(shù)分別為1,3,4,則
(單位:千元)應(yīng)抽取的人數(shù)分別為1,3,4,則![]() 0,1,2,3,
0,1,2,3,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
故![]() 的數(shù)學(xué)期望為
的數(shù)學(xué)期望為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)試討論函數(shù)![]() 的極值點(diǎn)的個(gè)數(shù);
的極值點(diǎn)的個(gè)數(shù);
(2)若![]() ,且
,且![]() 恒成立,求a的最大值.
恒成立,求a的最大值.
參考數(shù)據(jù):
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.588 | 2.303 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某健身館為響應(yīng)十九屆四中全會(huì)提出的“聚焦增強(qiáng)人民體質(zhì),健全促進(jìn)全民健身制度性舉措”,提高廣大市民對(duì)全民健身運(yùn)動(dòng)的參與程度,推出了讓健身館會(huì)員參與的健身促銷活動(dòng).
(1)為了解會(huì)員對(duì)促銷活動(dòng)的興趣程度,現(xiàn)從某周六參加該健身館健身活動(dòng)的會(huì)員中隨機(jī)采訪男性會(huì)員和女性會(huì)員各![]() 人,他們對(duì)于此次健身館健身促銷活動(dòng)感興趣的程度如下表所示:
人,他們對(duì)于此次健身館健身促銷活動(dòng)感興趣的程度如下表所示:
感興趣 | 無(wú)所謂 | 合計(jì) | |
男性 |
|
|
|
女性 |
|
|
|
合計(jì) |
|
|
|
根據(jù)以上數(shù)據(jù)能否有![]() 的把握認(rèn)為“對(duì)健身促銷活動(dòng)感興趣”與“性別”有關(guān)?
的把握認(rèn)為“對(duì)健身促銷活動(dòng)感興趣”與“性別”有關(guān)?
(參考公式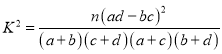 ,其中
,其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
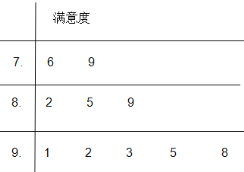
(2)在感興趣的會(huì)員中隨機(jī)抽取![]() 人對(duì)此次健身促銷活動(dòng)的滿意度進(jìn)行調(diào)查,以莖葉圖記錄了他們對(duì)此次健身促銷活動(dòng)滿意度的分?jǐn)?shù)(滿分
人對(duì)此次健身促銷活動(dòng)的滿意度進(jìn)行調(diào)查,以莖葉圖記錄了他們對(duì)此次健身促銷活動(dòng)滿意度的分?jǐn)?shù)(滿分![]() 分),如圖所示,若將此莖葉圖中滿意度分為“很滿意”(分?jǐn)?shù)不低于
分),如圖所示,若將此莖葉圖中滿意度分為“很滿意”(分?jǐn)?shù)不低于![]() 分)、“滿意”(分?jǐn)?shù)不低于平均分且低于
分)、“滿意”(分?jǐn)?shù)不低于平均分且低于![]() 分)、“基本滿意”(分?jǐn)?shù)低于平均分)三個(gè)級(jí)別.先從“滿意”和“很滿意”的會(huì)員中隨機(jī)抽取兩人參加回訪饋贈(zèng)活動(dòng),求這兩人中至少有一人是“很滿意”會(huì)員的概率.
分)、“基本滿意”(分?jǐn)?shù)低于平均分)三個(gè)級(jí)別.先從“滿意”和“很滿意”的會(huì)員中隨機(jī)抽取兩人參加回訪饋贈(zèng)活動(dòng),求這兩人中至少有一人是“很滿意”會(huì)員的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(I)當(dāng)a=2時(shí),求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(II)設(shè)函數(shù)![]() ,z.x.x.k討論
,z.x.x.k討論![]() 的單調(diào)性并判斷有無(wú)極值,有極值時(shí)求出極值.
的單調(diào)性并判斷有無(wú)極值,有極值時(shí)求出極值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為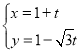 (
(![]() 為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系,曲線
軸正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的直角坐標(biāo)方程和直線
的直角坐標(biāo)方程和直線![]() 的普通方程;
的普通方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點(diǎn),設(shè)
兩點(diǎn),設(shè)![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱柱![]() 中,四邊形
中,四邊形![]() ,
,![]() 均為正方形,且
均為正方形,且![]() ,M為
,M為![]() 的中點(diǎn),N為
的中點(diǎn),N為![]() 的中點(diǎn).
的中點(diǎn).

(1)求證:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)設(shè)P是棱![]() 上一點(diǎn),若直線PM與平面
上一點(diǎn),若直線PM與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 的最小正周期為
的最小正周期為![]() ,將
,將![]() 的圖象向左平移
的圖象向左平移![]() 個(gè)單位后,所得圖象關(guān)于原點(diǎn)對(duì)稱,則函數(shù)
個(gè)單位后,所得圖象關(guān)于原點(diǎn)對(duì)稱,則函數(shù)![]() 的圖象( )
的圖象( )
A.關(guān)于直線![]() 對(duì)稱B.關(guān)于直線
對(duì)稱B.關(guān)于直線![]() 對(duì)稱
對(duì)稱
C.關(guān)于點(diǎn)(![]() ,0)對(duì)稱D.關(guān)于點(diǎn)(
,0)對(duì)稱D.關(guān)于點(diǎn)(![]() ,0)對(duì)稱
,0)對(duì)稱
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() ,
,![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在線段
在線段![]() 上,
上,![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,求點(diǎn)
,求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com