
【題目】已知函數(shù)![]() ,
,![]() .
.
(I)設(shè)![]() ,求
,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)若![]() 在
在![]() 處取得極大值,求實數(shù)
處取得極大值,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(I)單調(diào)增區(qū)間是![]() ,單調(diào)減區(qū)間是
,單調(diào)減區(qū)間是![]() .(II)
.(II)![]()
【解析】
試題分析:(I)![]() ,先求
,先求![]() 導(dǎo)函數(shù)
導(dǎo)函數(shù)![]() ,求導(dǎo)函數(shù)零點
,求導(dǎo)函數(shù)零點![]() ,列表分析導(dǎo)函數(shù)符號變化規(guī)律,確定單調(diào)區(qū)間(II)由題意得
,列表分析導(dǎo)函數(shù)符號變化規(guī)律,確定單調(diào)區(qū)間(II)由題意得![]() ,且
,且![]() 最大值;
最大值;![]() 最大值;而
最大值;而![]() 所以
所以![]() ,也可分類討論單調(diào)性變化規(guī)律
,也可分類討論單調(diào)性變化規(guī)律
試題解析:解:(I)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() .
.
當(dāng)![]() 時,在
時,在![]() 上
上![]() ,
,![]() 單調(diào)遞增;
單調(diào)遞增;
在![]() 上
上![]() ,
,![]() 單調(diào)遞減.
單調(diào)遞減.
∴![]() 的單調(diào)增區(qū)間是
的單調(diào)增區(qū)間是![]() ,單調(diào)減區(qū)間是
,單調(diào)減區(qū)間是![]() .
.
(II)∵![]() 在
在![]() 處取得極大值,∴
處取得極大值,∴![]() .
.
①當(dāng)![]() ,即
,即![]() 時,由(I)知
時,由(I)知![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
∴當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞減,不合題意;
單調(diào)遞減,不合題意;
②當(dāng)![]() ,即
,即![]() 時,由(I)知,
時,由(I)知,![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
∴當(dāng)![]() 時,
時,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
∴![]() 在
在![]() 處取得極小值,不合題意;
處取得極小值,不合題意;
③當(dāng)![]() ,即
,即![]() 時,由(I)知,
時,由(I)知,![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
∴當(dāng)![]() 時,
時,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
∴當(dāng)![]() 時,
時,![]() 取得極大值,滿足條件.
取得極大值,滿足條件.
綜上,實數(shù)![]() 的取值范圍是
的取值范圍是![]()


 名題金卷系列答案
名題金卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,游客從某旅游景區(qū)的景點![]() 處下上至
處下上至![]() 處有兩種路徑.一種是從
處有兩種路徑.一種是從![]() 沿直線步行到
沿直線步行到![]() ,另一種是先從
,另一種是先從![]() 沿索道乘纜車到
沿索道乘纜車到![]() ,然后從
,然后從![]() 沿直線步行到
沿直線步行到![]() .現(xiàn)有甲、乙兩位游客從
.現(xiàn)有甲、乙兩位游客從![]() 處下山,甲沿
處下山,甲沿![]() 勻速步行,速度為
勻速步行,速度為![]() .在甲出發(fā)
.在甲出發(fā)![]() 后,乙從
后,乙從![]() 乘纜車到
乘纜車到![]() ,在
,在![]() 處停留
處停留![]() 后,再從
后,再從![]() 勻速步行到
勻速步行到![]() ,假設(shè)纜車勻速直線運動的速度為
,假設(shè)纜車勻速直線運動的速度為![]() ,山路
,山路![]() 長為1260
長為1260![]() ,經(jīng)測量
,經(jīng)測量![]() ,
,![]() .
.

(1)求索道![]() 的長;
的長;
(2)問:乙出發(fā)多少![]() 后,乙在纜車上與甲的距離最短?
后,乙在纜車上與甲的距離最短?
(3)為使兩位游客在![]() 處互相等待的時間不超過
處互相等待的時間不超過![]() ,乙步行的速度應(yīng)控制在什么范圍內(nèi)?
,乙步行的速度應(yīng)控制在什么范圍內(nèi)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,ABCD是塊矩形硬紙板,其中AB=2AD,AD=![]() ,E為DC的中點,將它沿AE折成直二面角D-AE-B.
,E為DC的中點,將它沿AE折成直二面角D-AE-B.
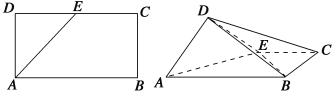
(1)求證:AD⊥平面BDE;
(2)求二面角B-AD-E的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,兩條公路AP與AQ夾角A為鈍角,其正弦值是![]()
![]() .甲乙兩人從A點出發(fā)沿著兩條公路進行搜救工作,甲沿著公路AP方向,乙沿著公路AQ方向.
.甲乙兩人從A點出發(fā)沿著兩條公路進行搜救工作,甲沿著公路AP方向,乙沿著公路AQ方向.

(1)當(dāng)甲前進5km的時候到達P處,同時乙到達Q處,通訊測得甲乙兩人相距![]()
![]() km,求乙在此時前進的距離AQ;
km,求乙在此時前進的距離AQ;
(2)甲在5公里處原地未動,乙回頭往A方向行走至M點收到甲發(fā)出的信號,此時M點看P、Q兩點的張角為![]() (張角為
(張角為![]() QMP)
QMP)![]() ,求甲乙兩人相距的距離MP的長.
,求甲乙兩人相距的距離MP的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校對高一年級學(xué)生寒假參加社區(qū)服務(wù)的次數(shù)進行了統(tǒng)計,隨機抽取了![]() 名學(xué)生作為樣本,得到這
名學(xué)生作為樣本,得到這![]() 名學(xué)生參加社區(qū)服務(wù)的次數(shù),根據(jù)此數(shù)據(jù)作出了頻率分布統(tǒng)計表和頻率分布直方圖如下:
名學(xué)生參加社區(qū)服務(wù)的次數(shù),根據(jù)此數(shù)據(jù)作出了頻率分布統(tǒng)計表和頻率分布直方圖如下:

(1)求表中![]() 的值和頻率分布直方圖中
的值和頻率分布直方圖中![]() 的值,并根據(jù)頻率分布直方圖估計該校高一學(xué)生寒假參加社區(qū)服務(wù)次數(shù)的中位數(shù);
的值,并根據(jù)頻率分布直方圖估計該校高一學(xué)生寒假參加社區(qū)服務(wù)次數(shù)的中位數(shù);
(2)如果用分層抽樣的方法從樣本服務(wù)次數(shù)在![]() 和
和![]() 的人中共抽取6人,再從這6人中選2人,求2人服務(wù)次數(shù)都在
的人中共抽取6人,再從這6人中選2人,求2人服務(wù)次數(shù)都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知A(4, 0),B(2, 2),C (6, 0),記△ABC的外接圓為⊙P.
(1)求⊙P的方程.
(2)對于線段PA上的任意一點G,是否存在以B為圓心的圓,在圓B上總能找到不同的兩點E、F,滿足![]() =
=![]() ,若存在,求圓B的半徑
,若存在,求圓B的半徑![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某廠有容量300噸的水塔一個,每天從早六點到晚十點供應(yīng)生活和生產(chǎn)用水,已知:該廠生活用水每小時10噸,工業(yè)用水總量![]() (噸)與時間
(噸)與時間![]() (單位:小時,規(guī)定早晨六點時
(單位:小時,規(guī)定早晨六點時![]() )的函數(shù)關(guān)系為
)的函數(shù)關(guān)系為![]() ,水塔的進水量有10級,第一級每小時進水10噸,以后每提高一級, 進水量增加10噸.若某天水塔原有水100噸,在供應(yīng)同時打開進水管.問該天進水量應(yīng)選擇幾級,既能保證該廠用水(即水塔中水不空),又不會使水溢出?
,水塔的進水量有10級,第一級每小時進水10噸,以后每提高一級, 進水量增加10噸.若某天水塔原有水100噸,在供應(yīng)同時打開進水管.問該天進水量應(yīng)選擇幾級,既能保證該廠用水(即水塔中水不空),又不會使水溢出?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com