
【題目】如圖,四棱錐 ![]() 中,底面ABCD為矩形,側(cè)面PAD為正三角形,且平面
中,底面ABCD為矩形,側(cè)面PAD為正三角形,且平面 ![]() ABCD平面, E為PD中點, AD=2.
ABCD平面, E為PD中點, AD=2.
(Ⅰ)求證:平面 ![]() 平面PCD;
平面PCD;
(Ⅱ)若二面角 ![]() 的平面角大小
的平面角大小 ![]() 滿足
滿足 ![]() ,求四棱錐
,求四棱錐 ![]() 的體積.
的體積.
【答案】解:(Ⅰ)取AD中點為O, BC中點為E,
由側(cè)面PAD為正三角形,且平面 ![]() 平面ABCD知
平面ABCD知 ![]() 平面ABCD,故
平面ABCD,故 ![]() ,
,
又 ![]() ,則
,則 ![]() 平面PAD,所以
平面PAD,所以 ![]() ,
,
又 ![]() ,則
,則 ![]() ,又E是PD中點,則
,又E是PD中點,則 ![]() ,
,
由線面垂直的判定定理知 ![]() 平面PCD,
平面PCD,
又 ![]() 平面AEC,故平面
平面AEC,故平面 ![]() 平面PCD.
平面PCD.
(Ⅱ)
如圖所示,建立空間直角坐標系 ![]() ,
,
令A(yù)B=a,則 ![]() .
.
由(Ⅰ)知 ![]() 為平面PCE的法向量,
為平面PCE的法向量,
令 ![]() 為平面PAC的法向量,
為平面PAC的法向量,
由于 ![]() 均與n垂直,
均與n垂直,
故 ![]() 即
即 ![]() 解得
解得 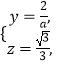
故 ![]() ,由
,由 
 ,解得
,解得 ![]() .
.
故四棱錐 ![]() 的體積
的體積 ![]()
【解析】(1)由平面與平面垂直的性質(zhì)可得直線與平面垂直,進而得到直線與直線垂直,利用直線與平面垂直的判定定理得到直線與平面垂直,一組相交直線分別垂直于同一平面,故可推出平面與平面垂直。
(2)將立體幾何坐標化,通過向量的方法,設(shè)出平面法向量,最終求得四棱錐的體積。
【考點精析】根據(jù)題目的已知條件,利用平面與平面垂直的判定的相關(guān)知識可以得到問題的答案,需要掌握一個平面過另一個平面的垂線,則這兩個平面垂直.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè) ![]() 為等比數(shù)列,
為等比數(shù)列, ![]() 為等差數(shù)列,且
為等差數(shù)列,且 ![]() =
= ![]() =
= ![]() ,若
,若 ![]() 是1,1,2,…,求
是1,1,2,…,求
(1)數(shù)列 ![]() 的通項公式
的通項公式
(2)數(shù)列 ![]() 的前10項的和.
的前10項的和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)用五點法畫出它在一個周期內(nèi)的閉區(qū)間上的圖象;
(2)指出![]() 的周期、振幅、初相、對稱軸;
的周期、振幅、初相、對稱軸;
(3)說明此函數(shù)圖象可由![]() 的圖象經(jīng)怎樣的變換得到.
的圖象經(jīng)怎樣的變換得到.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有一塊半徑為![]() 的正常數(shù))的半圓形空地,開發(fā)商計劃征地建一個矩形的游泳池
的正常數(shù))的半圓形空地,開發(fā)商計劃征地建一個矩形的游泳池![]() 和其附屬設(shè)施,附屬設(shè)施占地形狀是等腰
和其附屬設(shè)施,附屬設(shè)施占地形狀是等腰![]() ,其中
,其中![]() 為圓心,
為圓心, ![]() 在圓的直徑上,
在圓的直徑上, ![]() 在半圓周上,如圖.
在半圓周上,如圖.
(1)設(shè)![]() ,征地面積為
,征地面積為![]() ,求
,求![]() 的表達式,并寫出定義域;
的表達式,并寫出定義域;
(2)當![]() 滿足
滿足![]() 取得最大值時,開發(fā)效果最佳,求出開發(fā)效果最佳的角
取得最大值時,開發(fā)效果最佳,求出開發(fā)效果最佳的角![]() 的值,
的值,
求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線C: ![]() ,點
,點 ![]() 在x軸的正半軸上,過點M的直線
在x軸的正半軸上,過點M的直線 ![]() 與拋物線C相交于A,B兩點,O為坐標原點.
與拋物線C相交于A,B兩點,O為坐標原點.
(1)若 ![]() ,且直線
,且直線 ![]() 的斜率為1,求以AB為直徑的圓的方程;
的斜率為1,求以AB為直徑的圓的方程;
(2)是否存在定點M,使得不論直線 ![]() 繞點M如何轉(zhuǎn)動,
繞點M如何轉(zhuǎn)動, ![]() 恒為定值?
恒為定值?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() (e為自然對數(shù)的底).若函數(shù)g(x)=f(x)﹣kx恰好有兩個零點,則實數(shù)k的取值范圍是( )
(e為自然對數(shù)的底).若函數(shù)g(x)=f(x)﹣kx恰好有兩個零點,則實數(shù)k的取值范圍是( )
A.(1,e)
B.(e,10]
C.(1,10]
D.(10,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】袋中有a個黑球和b個白球,隨機地每次從中取出一球,每次取后不放回,記事件A為“直到第k次才取到黑球”,其中1≤k≤b;事件B為“第7次取出的球恰好是黑球”,其中1≤k≤b。
(Ⅰ)若a=5,b=3,k=2,求事件A發(fā)生的概率;
(Ⅱ)判斷事件B發(fā)生的概率是否隨k取值的變化而變化?并說明理由;
(Ⅲ)比較a=5,b=9時事件A發(fā)生的概率與a=5,b=10時事件A發(fā)生的概率的大小,并說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 、
、![]() 是兩條不同的直線,
是兩條不同的直線, ![]() ,
, ![]() ,
, ![]() 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若![]() ,
, ![]() ,則
,則![]() ②若
②若![]() ,
, ![]() ,
, ![]() ,則
,則![]()
③若![]() ,
, ![]() ,則
,則![]() ④若
④若![]() ,
, ![]() ,則
,則![]()
其中正確命題的序號是( ).
A. ①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】【2018河南南陽市一中上學(xué)期第三次月考】已知點![]() 為坐標原點,
為坐標原點, ![]() 是橢圓
是橢圓![]() 上的兩個動點,滿足直線
上的兩個動點,滿足直線![]() 與直線
與直線![]() 關(guān)于直線
關(guān)于直線![]() 對稱.
對稱.
(I)證明直線![]() 的斜率為定值,并求出這個定值;
的斜率為定值,并求出這個定值;
(II)求![]() 的面積最大時直線
的面積最大時直線![]() 的方程.
的方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com