
已知函數(shù)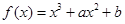 的圖象上一點P(1,0),且在P點處的切線與直線
的圖象上一點P(1,0),且在P點處的切線與直線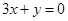 平行.
平行.
(1)求函數(shù) 的解析式;
的解析式;
(2)求函數(shù) 在區(qū)間[0,t](0<t<3)上的最大值和最小值;
在區(qū)間[0,t](0<t<3)上的最大值和最小值;
(3)在(1)的結(jié)論下,關(guān)于x的方程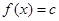 在區(qū)間[1,3]上恰有兩個相異的實根,求實數(shù)c的取值范圍
在區(qū)間[1,3]上恰有兩個相異的實根,求實數(shù)c的取值范圍
(1)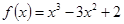 (2)答案見解析 (3)
(2)答案見解析 (3)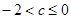
解析試題分析:(1)由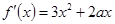 及曲線在
及曲線在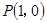 處的切線斜率為
處的切線斜率為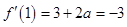 ,即可求得
,即可求得 ,又函數(shù)過
,又函數(shù)過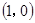 點,即可求的
點,即可求的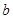 .
.
(2)由(1)易知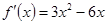 ,令
,令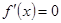 可得
可得 或
或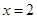 ,然后對
,然后對 進(jìn)行分類討論,確定函數(shù)
進(jìn)行分類討論,確定函數(shù) 在
在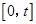 的單調(diào)性,即可求出函數(shù)
的單調(diào)性,即可求出函數(shù) 在
在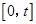
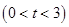 上的最大值和最小值;
上的最大值和最小值;
(3)構(gòu)造函數(shù)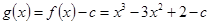 ,研究函數(shù)
,研究函數(shù)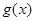 的單調(diào)性,列出該方程有兩個相異的實根的不等式組,求出實數(shù)
的單調(diào)性,列出該方程有兩個相異的實根的不等式組,求出實數(shù) 的取值范圍.
的取值范圍.
試題解析:(1)因為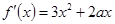 ,曲線在
,曲線在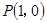 處的切線斜率為
處的切線斜率為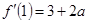 ,即
,即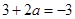 ,所以
,所以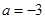 .
.
又函數(shù)過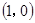 點,即
點,即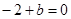 ,所以
,所以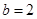 .
.
所以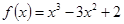 .
.
(2)由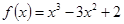 ,
,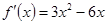 .
.
由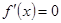 ,得
,得 或
或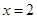 .
.
①當(dāng)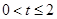 時,在區(qū)間
時,在區(qū)間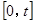 上
上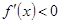 ,
, 在
在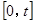 上是減函數(shù),
上是減函數(shù),
所以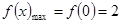 ,
,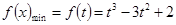 .
.
②當(dāng)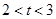 時,當(dāng)
時,當(dāng)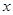 變化時,
變化時, 、
、 的變化情況見下表:
的變化情況見下表: