
【題目】為了解某品種一批樹苗生長情況,在該批樹苗中隨機抽取了容量為120的樣本,測量樹苗高度(單位:cm),經統計,其高度均在區間[19,31]內,將其按[19,21),[21,23),[23,25),[25,27),[27,29),[29,31]分成6組,制成如圖所示的頻率分布直方圖.其中高度為27 cm及以上的樹苗為優質樹苗.
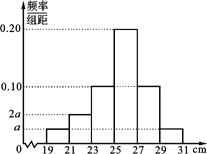
(1)求圖中a的值;
(2)已知所抽取的這120棵樹苗來自于A,B兩個試驗區,部分數據如下列聯表:
A試驗區 | B試驗區 | 合計 | |
優質樹苗 | 20 | ||
非優質樹苗 | 60 | ||
合計 |
將列聯表補充完整,并判斷是否有99.9%的把握認為優質樹苗與A,B兩個試驗區有關系,并說明理由;
(3)用樣本估計總體,若從這批樹苗中隨機抽取4棵,其中優質樹苗的棵數為X,求X的分布列和數學期望EX.
下面的臨界值表僅供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() .)
.)
【答案】(1)0.025;(2)見解析;(3)見解析
【解析】
(1)根據直方圖數據,有![]() ,從而可得結果;(2)根據直方圖完成列聯表,利用公式求得
,從而可得結果;(2)根據直方圖完成列聯表,利用公式求得![]() ,與臨界值比較即可得結果;(3)由已知,這批樹苗為優質樹苗的概率為
,與臨界值比較即可得結果;(3)由已知,這批樹苗為優質樹苗的概率為![]() ,且
,且![]() 服從二項分布
服從二項分布![]() ,由二項分布的期望公式可得結果.
,由二項分布的期望公式可得結果.
(1)根據直方圖數據,有![]() ,
,
解得![]() .
.
(2)根據直方圖可知,樣本中優質樹苗有![]() ,列聯表如下:
,列聯表如下:
A試驗區 | B試驗區 | 合計 | |
優質樹苗 | 10 | 20 | 30 |
非優質樹苗 | 60 | 30 | 90 |
合計 | 70 | 50 | 120 |
可得![]() .
.
所以,沒有99.9%的把握認為優質樹苗與A,B兩個試驗區有關系.
(3)由已知,這批樹苗為優質樹苗的概率為![]() ,且X服從二項分布B(4,
,且X服從二項分布B(4,![]() ),
),
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() .
.
所以X的分布列為:
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
故數學期望EX=![]() .
.


科目:高中數學 來源: 題型:
【題目】設二次函數![]() 滿足下列條件:當
滿足下列條件:當![]() 時,
時,![]() 的最小值為0,且
的最小值為0,且![]() 成立;當
成立;當![]() 時,
時,![]() 恒成立.
恒成立.
(1)求![]() 的解析式;
的解析式;
(2)若對![]() ,不等式
,不等式![]() 恒成立、求實數
恒成立、求實數![]() 的取值范圍;
的取值范圍;
(3)求最大的實數![]() ,使得存在實數
,使得存在實數![]() ,只要當
,只要當![]() 時,就有
時,就有![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某品種一批樹苗生長情況,在該批樹苗中隨機抽取了容量為120的樣本,測量樹苗高度(單位:cm),經統計,其高度均在區間[19,31]內,將其按[19,21),[21,23),[23,25),[25,27),[27,29),[29,31]分成6組,制成如圖所示的頻率分布直方圖.其中高度為27 cm及以上的樹苗為優質樹苗.
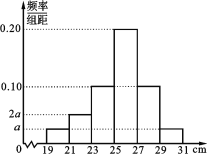
(1)求圖中a的值;
(2)已知所抽取的這120棵樹苗來自于A,B兩個試驗區,部分數據如下列聯表:
A試驗區 | B試驗區 | 合計 | |
優質樹苗 | 20 | ||
非優質樹苗 | 60 | ||
合計 |
將列聯表補充完整,并判斷是否有99.9%的把握認為優質樹苗與A,B兩個試驗區有關系,并說明理由;
(3)用樣本估計總體,若從這批樹苗中隨機抽取4棵,其中優質樹苗的棵數為X,求X的分布列和數學期望EX.
下面的臨界值表僅供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定橢圓C:![]() (a>b>0),稱圓C1:x2+y2=a2+b2為橢圓C的“伴隨圓”.已知橢圓C的離心率為
(a>b>0),稱圓C1:x2+y2=a2+b2為橢圓C的“伴隨圓”.已知橢圓C的離心率為![]() ,且經過點(0,1).
,且經過點(0,1).
(1)求實數a,b的值;
(2)若過點P(0,m)(m>0)的直線l與橢圓C有且只有一個公共點,且l被橢圓C的伴隨圓C1所截得的弦長為2![]() ,求實數m的值.
,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在著名的漢諾塔問題中,有三根高度相同的柱子和一些大小及顏色各不相同的圓盤,三根柱子分別為起始柱、輔助柱及目標柱.已知起始柱上套有![]() 個圓盤,較大的圓盤都在較小的圓盤下面.現把圓盤從起始柱全部移到目標柱上,規則如下:每次只能移動一個圓盤,且每次移動后,每根柱上較大的圓盤不能放在較小的圓盤上面,規定一個圓盤從任一根柱上移動到另一根柱上為一次移動.若將
個圓盤,較大的圓盤都在較小的圓盤下面.現把圓盤從起始柱全部移到目標柱上,規則如下:每次只能移動一個圓盤,且每次移動后,每根柱上較大的圓盤不能放在較小的圓盤上面,規定一個圓盤從任一根柱上移動到另一根柱上為一次移動.若將![]() 個圓盤從起始柱移動到目標柱上最少需要移動的次數記為
個圓盤從起始柱移動到目標柱上最少需要移動的次數記為![]() ,則
,則![]() __________,
__________,![]() __________.
__________.
![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 的定義域為
的定義域為![]() ,滿足對任意
,滿足對任意![]() ,
,![]() ,有
,有![]() ,則稱
,則稱![]() 為
為![]() 型函數;若函數
型函數;若函數![]() 的定義域為
的定義域為![]() ,滿足對任意
,滿足對任意![]() ,
,![]() 恒成立,且對任意
恒成立,且對任意![]() ,
,![]() ,有
,有![]() ,則稱
,則稱![]() 為對數
為對數![]() 型函數.
型函數.
(1)當函數![]() 時,判斷
時,判斷![]() 是否為
是否為![]() 型函數,并說明理由.
型函數,并說明理由.
(2)當函數![]() 時,證明:
時,證明:![]() 是對數
是對數![]() 型函數.
型函數.
(3)若函數![]() 是
是![]() 型函數,且滿足對任意
型函數,且滿足對任意![]() ,有
,有![]() ,問
,問![]() 是否為對數
是否為對數![]() 型函數?若是,加以證明;若不是,請說明理由.
型函數?若是,加以證明;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某中學高三文科班學生共有800人參加了數學與地理的水平測試,學校決定利用隨機數表法從中抽取100人進行成績抽樣調查,先將800人按001,002,…,800進行編號.
(1)如果從第8行第7列的數開始向右讀,請你依次寫出最先檢查的3個人的編號;
(下面摘取了第7行到第9行)

(2)抽取的100人的數學與地理的水平測試成績如下表:成績分為優秀、良好、及格三個等級;橫向,縱向分別表示地理成績與數學成績,例如:表中數學成績為良好的共有![]() .
.
①若在該樣本中,數學成績優秀率是![]() ,求
,求![]() 的值:
的值:
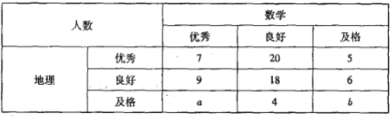
②在地理成績及格的學生中,已知![]() ,求數學成績優秀的人數比及格的人數少的概率.
,求數學成績優秀的人數比及格的人數少的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的![]() ,
,![]() ,
,![]() 三個不同車間生產同一產品的數量(單位:件)如下表所示.質檢人員用分層抽樣的方法從這些產品中共抽取6件樣品進行檢測:
三個不同車間生產同一產品的數量(單位:件)如下表所示.質檢人員用分層抽樣的方法從這些產品中共抽取6件樣品進行檢測:
車間 |
|
|
|
數量 | 50 | 150 | 100 |
(1)求這6件樣品中來自![]() ,
,![]() ,
,![]() 各車間產品的數量;
各車間產品的數量;
(2)若在這6件樣品中隨機抽取2件進行進一步檢測,求這2件產品來自相同車間的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com