
���タ(xi��n)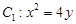 ���c(di��n)
���c(di��n) ��
�� ̎���о�(xi��n)��ֱ�ཻ���c(di��n)
̎���о�(xi��n)��ֱ�ཻ���c(di��n)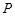 ��ֱ��(xi��n)
��ֱ��(xi��n)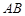 �c�E�A
�c�E�A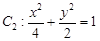 �ཻ��
�ཻ�� ��
�� ���c(di��n)��
���c(di��n)��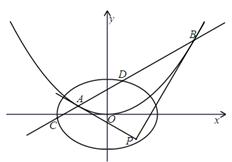
��1�����タ(xi��n) �Ľ��c(di��n)
�Ľ��c(di��n)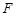 �c�E�A
�c�E�A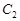 �����c(di��n)
�����c(di��n)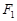 �ľ��x��
�ľ��x��
��2���O(sh��)�c(di��n)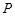 ��ֱ��(xi��n)
��ֱ��(xi��n)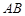 �ľ��x��
�ľ��x��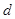 ��ԇ��(w��n)���Ƿ����ֱ��(xi��n)
��ԇ��(w��n)���Ƿ����ֱ��(xi��n)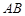 ��ʹ��
��ʹ��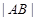 ��
��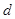 ��
��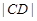 �ɵȱȔ�(sh��)�У������ڣ���ֱ��(xi��n)
�ɵȱȔ�(sh��)�У������ڣ���ֱ��(xi��n)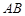 �ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
��1��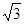 ;��2��������.
;��2��������.
����ԇ�}��������1���քe������タ(xi��n)�c�E�A�Ľ��c(di��n)�����Ã��c(di��n)�g���x��ʽ��⣻��2���O(sh��)ֱ��(xi��n) �c���タ(xi��n)�ཻ��
�c���タ(xi��n)�ཻ��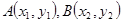 �c�E�A�ཻ��
�c�E�A�ཻ��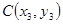 ,
,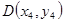 ,����ֱ��(xi��n)�c���タ(xi��n)����(li��n)�����õ�
,����ֱ��(xi��n)�c���タ(xi��n)����(li��n)�����õ�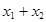 ��
��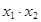 Ȼ������
Ȼ������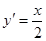 ,����о�(xi��n)
,����о�(xi��n)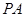 ��
��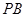 ��б�ʣ������о�(xi��n)��ֱ��
��б�ʣ������о�(xi��n)��ֱ��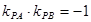 ,���m,Ȼ��քe�O(sh��)���^(gu��)
,���m,Ȼ��քe�O(sh��)���^(gu��)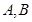 �c(di��n)���о�(xi��n)���̣�������c(di��n)
�c(di��n)���о�(xi��n)���̣�������c(di��n)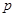 ������(bi��o)�������c(di��n)��ֱ��(xi��n)�ľ��x��ʽ��
������(bi��o)�������c(di��n)��ֱ��(xi��n)�ľ��x��ʽ��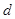 ,ֱ��(xi��n)�c����(xi��n)�ཻ�����L(zh��ng)��ʽ��
,ֱ��(xi��n)�c����(xi��n)�ཻ�����L(zh��ng)��ʽ��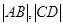 ,��
,��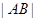 ��
��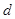 ��
��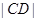 �ɵȱȔ�(sh��)�У��t
�ɵȱȔ�(sh��)�У��t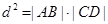 ,����(ji��n)��ʽ��ͨ�^(gu��)
,����(ji��n)��ʽ��ͨ�^(gu��)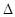 �����̌�(sh��)����r.
�����̌�(sh��)����r.
ԇ�}��������I�����タ(xi��n)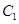 �Ľ��c(di��n)
�Ľ��c(di��n)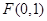 �� 1��
�� 1��
�E�A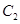 �����c(di��n)
�����c(di��n)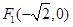 �� 2��
�� 2��
�t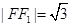 �� 3��
�� 3��
��II���O(sh��)ֱ��(xi��n) ��
��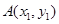 ��
�� ��
��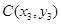 ��
��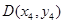 ��
��
��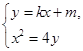 ����
����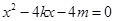 �� 4��
�� 4��
��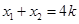 ��
��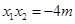 ��
��
��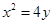 ����
����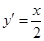 ��
��
���о�(xi��n)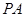 ��
��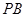 ��б�ʷքe��
��б�ʷքe��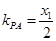 ��
��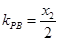 ��
��
����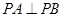 ����
����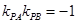 ��
��
��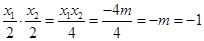 ��
��
��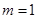 ���@�f(shu��)��ֱ��(xi��n)
���@�f(shu��)��ֱ��(xi��n)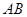 �^(gu��)���タ(xi��n)
�^(gu��)���タ(xi��n)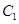 �Ľ��c(di��n)
�Ľ��c(di��n)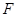 �� 7��
�� 7��
��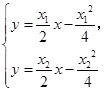 ����
����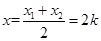 ��
��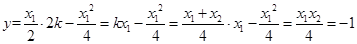 ,��
,��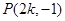 �� 8��
�� 8��
�����c(di��n)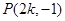 ��ֱ��(xi��n)
��ֱ��(xi��n)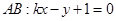 �ľ��x
�ľ��x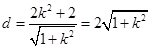 . 9��
. 9��
�� ����
����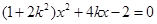 �� 10��
�� 10��
�Ķ�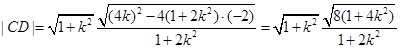 �� 11��
�� 11��
ͬ����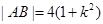 �� 12��
�� 12��
��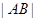 ��
��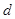 ��
��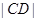 �ɵȱȔ�(sh��)�У��t
�ɵȱȔ�(sh��)�У��t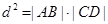 �� 13��
�� 13��
��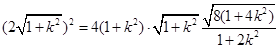 ��
��
����(ji��n)��������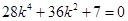 ���˷��̟o(w��)��(sh��)����
���˷��̟o(w��)��(sh��)����
���Բ�����ֱ��(xi��n)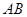 ��ʹ��
��ʹ��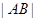 ��
��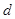 ��
��

 ���ƽ��o����(y��u)��(y��u)�x����ĩ�_��100��ϵ�д�
���ƽ��o����(y��u)��(y��u)�x����ĩ�_��100��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪��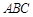 �ăɂ�(g��)��c(di��n)
�ăɂ�(g��)��c(di��n)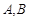 ������(bi��o)�քe��
������(bi��o)�քe��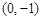 ��
��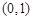 ����
����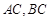 ����ֱ��(xi��n)��б��֮�e����
����ֱ��(xi��n)��б��֮�e����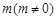 ��
��
��1������c(di��n)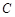 ��܉�E
��܉�E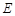 �ķ��̣����Д�܉�E
�ķ��̣����Д�܉�E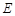 ��ηN�A�F����(xi��n)��
��ηN�A�F����(xi��n)��
��2����(d��ng)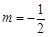 �r(sh��)���^(gu��)�c(di��n)
�r(sh��)���^(gu��)�c(di��n)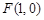 ��ֱ��(xi��n)
��ֱ��(xi��n)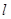 ������(xi��n)
������(xi��n)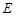 ��
��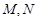 ���c(di��n)���O(sh��)�c(di��n)
���c(di��n)���O(sh��)�c(di��n)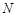 �P(gu��n)��
�P(gu��n)��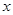 �S��(du��)�Q(ch��ng)�c(di��n)��
�S��(du��)�Q(ch��ng)�c(di��n)��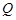 (
(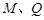 ���غ�)�� ԇ��(w��n)��ֱ��(xi��n)
���غ�)�� ԇ��(w��n)��ֱ��(xi��n)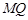 �c
�c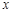 �S�Ľ��c(di��n)�Ƿ��Ƕ��c(di��n)�����ǣ�������c(di��n)�������ǣ�Ո(q��ng)�f(shu��)������.
�S�Ľ��c(di��n)�Ƿ��Ƕ��c(di��n)�����ǣ�������c(di��n)�������ǣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D,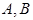 �ǙE�A
�ǙE�A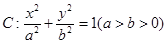 ��������c(di��n),�E�A
��������c(di��n),�E�A ���x���ʞ�
���x���ʞ�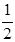 ,�Ҝ�(zh��n)��(xi��n)
,�Ҝ�(zh��n)��(xi��n)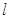 �ķ��̞�
�ķ��̞�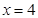 .
.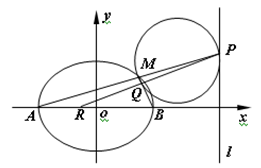
��1����E�A���̣�
��2���O(sh��)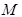 �ǙE�A
�ǙE�A �Ϯ���
�Ϯ���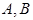 ��һ�c(di��n),ֱ��(xi��n)
��һ�c(di��n),ֱ��(xi��n)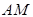 ��
��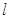 ���c(di��n)
���c(di��n)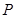 ,��
,��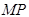 ��ֱ���ĈAӛ��
��ֱ���ĈAӛ��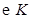 . ����
. ����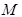 ǡ���ǙE�A
ǡ���ǙE�A ������c(di��n),��
������c(di��n),��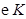 ��ֱ��(xi��n)
��ֱ��(xi��n)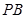 ���õ����L(zh��ng)��
���õ����L(zh��ng)��
���O(sh��)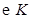 �cֱ��(xi��n)
�cֱ��(xi��n)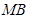 �����c(di��n)
�����c(di��n)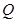 ,ԇ�C��:ֱ��(xi��n)
,ԇ�C��:ֱ��(xi��n)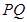 �c
�c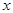 �S�Ľ��c(di��n)
�S�Ľ��c(di��n)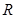 �鶨�c(di��n),����ԓ���c(di��n)������(bi��o).
�鶨�c(di��n),����ԓ���c(di��n)������(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪?ji��ng)�ֱ��(xi��n)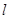 �c�E�A
�c�E�A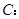
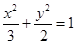 ����
����
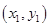 ��
��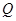
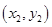 �ɲ�ͬ�c(di��n)���ҡ�
�ɲ�ͬ�c(di��n)���ҡ�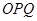 ����e
����e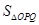 =
=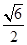 ������
������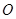 ������(bi��o)ԭ�c(di��n).
������(bi��o)ԭ�c(di��n).
��1���C��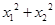 ��
��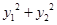 ���鶨ֵ��
���鶨ֵ��
��2���O(sh��)��(xi��n)��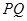 �����c(di��n)��
�����c(di��n)��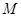 ����
����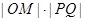 �����ֵ��
�����ֵ��
��3���E�A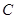 ���Ƿ�����c(di��n)
���Ƿ�����c(di��n) ��ʹ��
��ʹ��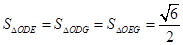 �������ڣ��Д��
�������ڣ��Д��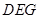 ���Π�������ڣ�Ո(q��ng)�f(shu��)������.
���Π�������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��1����֪�c(di��n)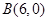 ��
�� ���^(gu��)�c(di��n)
���^(gu��)�c(di��n) ��ֱ��(xi��n)
��ֱ��(xi��n)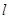 �c�^(gu��)�c(di��n)
�c�^(gu��)�c(di��n) ��ֱ��(xi��n)
��ֱ��(xi��n)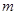 �ཻ���c(di��n)
�ཻ���c(di��n) ���O(sh��)ֱ��(xi��n)
���O(sh��)ֱ��(xi��n)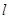 ��б�ʞ�
��б�ʞ�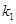 ��ֱ��(xi��n)
��ֱ��(xi��n)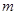 ��б�ʞ�
��б�ʞ�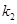 �����
�����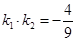 �����c(di��n)
�����c(di��n) ��܉�E��
��܉�E��
��2�������Ҷ����C�����������ƽ�־�(xi��n)����������� �У�
�У�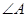 �����ƽ�־�(xi��n)
�����ƽ�־�(xi��n)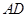 �c߅
�c߅ �����L(zh��ng)��(xi��n)�ཻ���c(di��n)
�����L(zh��ng)��(xi��n)�ཻ���c(di��n)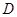 ���t
���t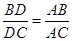 .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A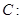
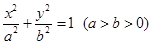 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��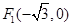 ��
��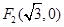 ���E�A�ϵ��c(di��n)
���E�A�ϵ��c(di��n) �M(m��n)��
�M(m��n)��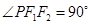 ����
����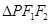 ����e
����e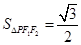 ��
��
������E�A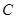 �ķ��̣�
�ķ��̣�
�����Ƿ����ֱ��(xi��n)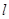 ��ʹ
��ʹ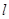 �c�E�A
�c�E�A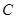 ���ڲ�ͬ�ă��c(di��n)
���ڲ�ͬ�ă��c(di��n)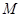 ��
�� ���Ҿ�(xi��n)��
���Ҿ�(xi��n)��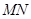 ǡ��ֱ��(xi��n)
ǡ��ֱ��(xi��n)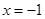 ƽ�֣������ڣ����
ƽ�֣������ڣ����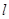 ��б��ȡֵ�������������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
��б��ȡֵ�������������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�A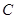 �^(gu��)���c(di��n)
�^(gu��)���c(di��n)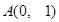 ���A��
���A��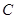 �ڒ��タ(xi��n)
�ڒ��タ(xi��n)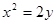 �ϣ�
�ϣ�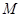 ��
��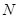 ��A
��A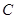 �c
�c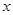 �S�Ľ��c(di��n)��
�S�Ľ��c(di��n)��
��1����(d��ng)�A��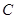 �ǒ��タ(xi��n)����c(di��n)�r(sh��)�����タ(xi��n)��(zh��n)��(xi��n)��ԓ�A�صõ����L(zh��ng)��
�ǒ��タ(xi��n)����c(di��n)�r(sh��)�����タ(xi��n)��(zh��n)��(xi��n)��ԓ�A�صõ����L(zh��ng)��
��2����(d��ng)�A��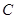 �ڒ��タ(xi��n)���\(y��n)��(d��ng)�r(sh��)��
�ڒ��タ(xi��n)���\(y��n)��(d��ng)�r(sh��)��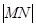 �Ƿ��һ��ֵ��Ո(q��ng)�C����ĽY(ji��)Փ��
�Ƿ��һ��ֵ��Ո(q��ng)�C����ĽY(ji��)Փ��
��3����(d��ng)�A��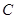 �ڒ��タ(xi��n)���\(y��n)��(d��ng)�r(sh��)��ӛ
�ڒ��タ(xi��n)���\(y��n)��(d��ng)�r(sh��)��ӛ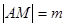 ��
��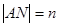 ����
����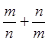 �����ֵ��������˕r(sh��)�A
�����ֵ��������˕r(sh��)�A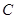 �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)F1��F2�քe�ǙE�AE��x2��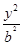 ��1(0<b<1)�����ҽ��c(di��n)���^(gu��)F1��ֱ��(xi��n)l�cE�ཻ��A��B���c(di��n)����|AF2|��|AB|��|BF2|�ɵȲ(sh��)�У�
��1(0<b<1)�����ҽ��c(di��n)���^(gu��)F1��ֱ��(xi��n)l�cE�ཻ��A��B���c(di��n)����|AF2|��|AB|��|BF2|�ɵȲ(sh��)�У�
(1)��|AB|��
(2)��ֱ��(xi��n)l��б�ʞ�1����b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�x����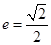 �ęE�A
�ęE�A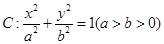 һ��(g��)���c(di��n)��
һ��(g��)���c(di��n)��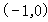 .
.
(1)��E�A �ķ��̣�
�ķ��̣�
(2) ��б�ʞ�1��ֱ��(xi��n) ���E�A
���E�A ��
�� ���c(di��n),��
���c(di��n),��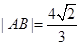 ����ֱ��(xi��n)
����ֱ��(xi��n) ����.
����.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com