
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() 為
為![]() 上一點.
上一點.
(1)若![]() 平面
平面![]() ,試說明點
,試說明點![]() 的位置并證明的結論;
的位置并證明的結論;
(2)若![]() 為
為![]() 的中點,
的中點,![]() 平面
平面![]() ,且
,且![]() ,
,
求二面角![]() 的余弦值.
的余弦值.
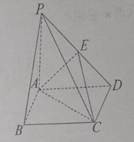
【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)當點![]() 為
為![]() 中點時有
中點時有![]() ,連接
,連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,由
,由![]() 為菱形得
為菱形得![]() 是
是![]() 的中點,由三角形的中位線性質可得
的中點,由三角形的中位線性質可得![]() ,即可證明
,即可證明![]() ;(2)以
;(2)以![]() 為坐標原點,分別以
為坐標原點,分別以![]() 為
為![]() 軸和
軸和![]() 軸建立空間直角坐標系,分別求得平面
軸建立空間直角坐標系,分別求得平面![]() 的法向量與平面
的法向量與平面![]() 的法向量,結合圖形得二面角
的法向量,結合圖形得二面角![]() 為銳二面角,即可求得二面角
為銳二面角,即可求得二面角![]() 的余弦值.
的余弦值.
試題解析:(1)當點![]() 為
為![]() 中點時有
中點時有![]() ,證明如下:
,證明如下:
連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .
.
由菱形性質知點![]() 是
是![]() 的中點.
的中點.
∴![]()
又∵![]()
∴![]() .
.
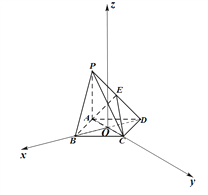
(2)由題意,以![]() 為坐標原點,分別以
為坐標原點,分別以![]() 為
為![]() 軸和
軸和![]() 軸建立如圖所示的空間直角坐標系,設
軸建立如圖所示的空間直角坐標系,設![]() ,則由條件易知
,則由條件易知![]() ,所以,
,所以,![]() .
.
∴![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則![]() .
.
∴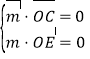 ,即
,即![]() ,令
,令![]() ,則
,則![]() ,所以,
,所以,![]()
同理可求平面![]() 的法向量
的法向量![]() .
.
所以,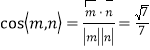 .
.
由圖可知,二面角![]() 為銳二面角,故其余弦值為
為銳二面角,故其余弦值為![]()


 每課必練系列答案
每課必練系列答案科目:高中數學 來源: 題型:
【題目】下列說法:
①集合{x∈N|x3=x}用列舉法表示為{-1,0,1};
②實數集可以表示為{x|x為所有實數}或{R};
③方程組![]() 的解集為{x=1,y=2}.
的解集為{x=1,y=2}.
其中正確的有( )
A.3個B.2個
C.1個D.0個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為了對新研發的一種產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價 | 4 | 6 | 7 | 8 | 10 |
銷量 | 60 | 50 | 45 | 30 | 20 |
(1) 請根據上表提供的數據畫出散點圖,并判斷是正相關還是負相關;
(2) 求出![]() 關于
關于![]() 的回歸直線方程,若單價為9元時,預測其銷量為多少?
的回歸直線方程,若單價為9元時,預測其銷量為多少?
(參考公式:回歸直線方程中公式 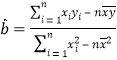 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() .將四邊形
.將四邊形![]() 沿對角線
沿對角線![]() 折成四面體
折成四面體![]() ,使平面
,使平面![]() 平面
平面![]() ,則下列結論中正確的結論個數是( )
,則下列結論中正確的結論個數是( )


①![]() ;②
;②![]() ;
;
③![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ;
;
④四面體![]() 的體積為
的體積為![]() .
.
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表數據為某地區某種農產品的年產量x(單位:噸)及對應銷售價格y(單位:千元/噸) .
x | 1 | 2 | 3 | 4 | 5 |
y | 70 | 65 | 55 | 38 | 22 |
(1)若y與x有較強的線性相關關系,根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程.
(2)若該農產品每噸的成本為13.1千元,假設該農產品可全部賣出,利用上問所求的回歸方程,預測當年產量為多少噸時,年利潤Z最大?
(參考公式:回歸直線方程為![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
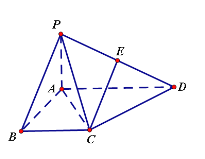
【題目】如圖,四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() .
.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() //平面
//平面![]() ?若存在,請確定
?若存在,請確定![]() 點的位置;若不存在,請說明理由.
點的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 過橢圓
過橢圓![]() 的右焦點
的右焦點![]() ,拋物線
,拋物線![]() 的焦點為橢圓
的焦點為橢圓![]() 的上頂點,且
的上頂點,且![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() 在直線
在直線![]() 上的射影依次為
上的射影依次為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() ,當
,當![]() 變化時,證明:
變化時,證明: ![]() 為定值;
為定值;
(3)當![]() 變化時,直線
變化時,直線![]() 與
與![]() 是否相交于定點?若是,請求出定點的坐標,并給予證明;否則,說明理由.
是否相交于定點?若是,請求出定點的坐標,并給予證明;否則,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間租賃甲、乙兩種設備生產A,B兩類產品,甲種設備每天能生產A類產品8件和B類產品15件,乙種設備每天能生產A類產品10件和B類產品25件,已知設備甲每天的租賃費300元,設備乙每天的租賃費400元,現車間至少要生產A類產品100件,B類產品200件,所需租賃費最少為__元![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com