
【題目】已知A、B分別為橢圓E:![]() (a>1)的左、右頂點,G為E的上頂點,
(a>1)的左、右頂點,G為E的上頂點,![]() ,P為直線x=6上的動點,PA與E的另一交點為C,PB與E的另一交點為D.
,P為直線x=6上的動點,PA與E的另一交點為C,PB與E的另一交點為D.
(1)求E的方程;
(2)證明:直線CD過定點.
【答案】(1)![]() ;(2)證明詳見解析.
;(2)證明詳見解析.
【解析】
(1)由已知可得:![]() ,
, ![]() ,
,![]() ,即可求得
,即可求得![]() ,結合已知即可求得:
,結合已知即可求得:![]() ,問題得解.
,問題得解.
(2)設![]() ,可得直線
,可得直線![]() 的方程為:
的方程為:![]() ,聯立直線
,聯立直線![]() 的方程與橢圓方程即可求得點
的方程與橢圓方程即可求得點![]() 的坐標為
的坐標為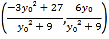 ,同理可得點
,同理可得點![]() 的坐標為
的坐標為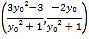 ,當
,當![]() 時,可表示出直線
時,可表示出直線![]() 的方程,整理直線
的方程,整理直線![]() 的方程可得:
的方程可得: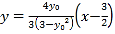 即可知直線過定點
即可知直線過定點![]() ,當
,當![]() 時,直線
時,直線![]() :
:![]() ,直線過點
,直線過點![]() ,命題得證.
,命題得證.
(1)依據題意作出如下圖象:
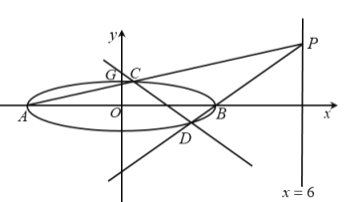
由橢圓方程![]() 可得:
可得:![]() ,
, ![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() 橢圓方程為:
橢圓方程為:![]()
(2)證明:設![]() ,
,
則直線![]() 的方程為:
的方程為:![]() ,即:
,即:![]()
聯立直線![]() 的方程與橢圓方程可得:
的方程與橢圓方程可得: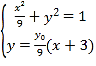 ,整理得:
,整理得:
![]() ,解得:
,解得:![]() 或
或![]()
將![]() 代入直線
代入直線![]() 可得:
可得:![]()
所以點![]() 的坐標為
的坐標為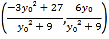 .
.
同理可得:點![]() 的坐標為
的坐標為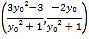
當![]() 時,
時,
![]() 直線
直線![]() 的方程為:
的方程為: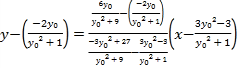 ,
,
整理可得: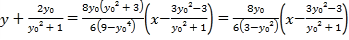
整理得: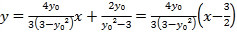
所以直線![]() 過定點
過定點![]() .
.
當![]() 時,直線
時,直線![]() :
:![]() ,直線過點
,直線過點![]() .
.
故直線CD過定點![]() .
.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:高中數學 來源: 題型:
【題目】新冠肺炎期間某商場開通三種平臺銷售商品,收集一月內的數據如圖1;為了解消費者對各平臺銷售方式的滿意程度,該商場用分層抽樣的方法抽取4%的顧客進行滿意度調查,得到的數據如圖2.下列說法錯誤的是( )
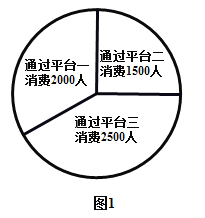
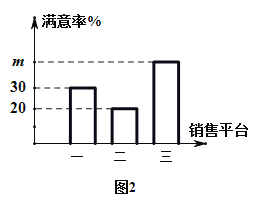
A.樣本容量為240
B.若樣本中對平臺三滿意的人數為40,則![]()
C.總體中對平臺二滿意的消費者人數約為300
D.樣本中對平臺一滿意的人數為24人
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4-4:坐標系與參數方程)
已知曲線C的極坐標方程是ρ=2cosθ,以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線L的參數方程是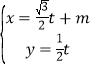 (t為參數).
(t為參數).
(1)求曲線C的直角坐標方程和直線L的普通方程;
(2)設點P(m,0),若直線L與曲線C交于A,B兩點,且|PA||PB|=1,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南宋數學家楊輝在所著的《詳解九章算法》一書中用如圖所示的三角形解釋二項展開式的系數規律,去掉所有為1的項,依次構成2,3,3,4,6,4,5,10,10,5,6…,則此數列的前50項和為( )

A.2025B.3052C.3053D.3049
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 為圓錐的頂點,
為圓錐的頂點,![]() 是圓錐底面的圓心,
是圓錐底面的圓心,![]() 是底面的內接正三角形,
是底面的內接正三角形,![]() 為
為![]() 上一點,∠APC=90°.
上一點,∠APC=90°.
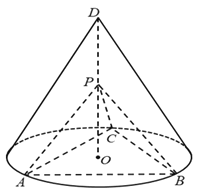
(1)證明:平面PAB⊥平面PAC;
(2)設DO=![]() ,圓錐的側面積為
,圓錐的側面積為![]() ,求三棱錐PABC的體積.
,求三棱錐PABC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C1:![]() (a>b>0)的右焦點F與拋物線C2的焦點重合,C1的中心與C2的頂點重合.過F且與x軸重直的直線交C1于A,B兩點,交C2于C,D兩點,且|CD|=
(a>b>0)的右焦點F與拋物線C2的焦點重合,C1的中心與C2的頂點重合.過F且與x軸重直的直線交C1于A,B兩點,交C2于C,D兩點,且|CD|=![]() |AB|.
|AB|.
(1)求C1的離心率;
(2)若C1的四個頂點到C2的準線距離之和為12,求C1與C2的標準方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱柱ABC-A1B1C1的底面是正三角形,側面BB1C1C是矩形,M,N分別為BC,B1C1的中點,P為AM上一點,過B1C1和P的平面交AB于E,交AC于F.
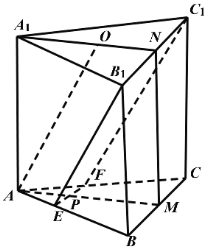
(1)證明:AA1∥MN,且平面A1AMN⊥EB1C1F;
(2)設O為△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直線B1E與平面A1AMN所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為拋物線
為拋物線![]() 的焦點,過
的焦點,過![]() 的動直線交拋物線
的動直線交拋物線![]() 于
于![]() ,
,![]() 兩點.當直線與
兩點.當直線與![]() 軸垂直時,
軸垂直時,![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)設直線![]() 的斜率為1且與拋物線的準線
的斜率為1且與拋物線的準線![]() 相交于點
相交于點![]() ,拋物線
,拋物線![]() 上存在點
上存在點![]() 使得直線
使得直線![]() ,
,![]() ,
,![]() 的斜率成等差數列,求點
的斜率成等差數列,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十五巧板、又稱益智圖,為清朝浙江省德清知縣童葉庚在同治年間所發明,它能拼出草木、花果、鳥獸、魚蟲、文字等圖案.十五巧板由十五塊板組成一個大正方形(如圖1),其中標號為2,3,4,5的小板均為等腰直角三角形,圖2是用十五巧板拼出的2019年生肖豬的圖案,則從生肖豬圖案中任取一點,該點恰好取自陰影部分中的概率為______.
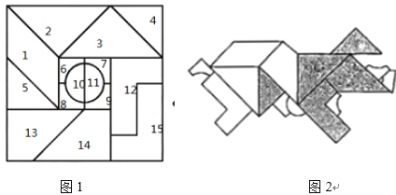
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com