
【題目】如圖,在正四棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中點,平面
的中點,平面![]() 與直線
與直線![]() 相交于點
相交于點![]() .
.
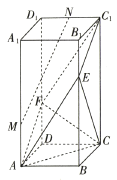
(1)證明:直線![]() 平面
平面![]() .
.
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)推導出![]() ,
,![]() ,設點
,設點![]() 為
為![]() 的中點,連結
的中點,連結![]() ,
,![]() ,推導出
,推導出![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,從而平面
,從而平面![]() 平面
平面![]() ,由此能證明
,由此能證明![]() 平面
平面![]() .
.
(2)以![]() 為原點,
為原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系,利用向量法能求出二面角
軸,建立空間直角坐標系,利用向量法能求出二面角![]() 的正弦值.
的正弦值.
解:(1)證明:![]() 平面
平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() ,由題意得
,由題意得![]() ,
,
設點![]() 為
為![]() 的中點,連結
的中點,連結![]() ,
,![]() ,
,
![]() 是棱
是棱![]() 的中點,
的中點,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(2)解:![]() ,
,![]() ,如圖,以
,如圖,以![]() 為原點,
為原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,
![]() ,0,
,0,![]() ,
,![]() ,1,
,1,![]() ,
,![]() ,0,
,0,![]() ,
,![]() 1,
1,![]() ,
,
![]()
![]() ,1,
,1,![]() ,
,![]() ,1,
,1,![]() ,
,![]() ,0,
,0,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
則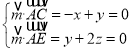 ,取
,取![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
則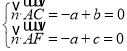 ,取
,取![]() ,得
,得![]() ,1,
,1,![]() ,
,
設二面角![]() 的平面角為
的平面角為![]() ,
,
由![]() ,
,
![]() ,
,
![]() 二面角
二面角![]() 的正弦值為
的正弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知三棱柱![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點,
的中點,![]() .
.
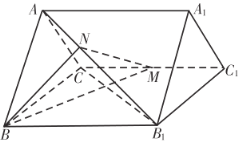
(1)求證:![]() 平面
平面![]() ;
;
(2)條件①:直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ;
;
條件②:![]() 為銳角,三棱錐
為銳角,三棱錐![]() 的體積為
的體積為![]() .
.
在以上兩個條件中任選一個,補充在下面的問題中,并解決該問題:
若平面![]() 平面
平面![]() ,______,求平面
,______,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果執行程序框圖,輸入正整數![]() ,
,![]() ,滿足
,滿足![]() ,那么輸出的
,那么輸出的![]() 等于( ).
等于( ).
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/25/2492401463009280/2492946029182977/STEM/3a3c20c7c34c41528daf48813411739a.png]
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正四棱錐![]() 底面的四個頂點
底面的四個頂點![]() ,
,![]() ,
,![]() ,
,![]() 在球
在球![]() 的同一個大圓上,點
的同一個大圓上,點![]() 在球面上,且已知
在球面上,且已知![]() .
.
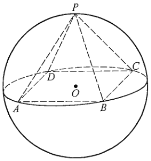
(1)求球![]() 的表面積;
的表面積;
(2)設![]() 為
為![]() 中點,求異面直線
中點,求異面直線![]() 與
與![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙曲線C的漸近線方程為![]() ,一個焦點為F(0,﹣8),則該雙曲線的標準方程為_____.已知點A(﹣6,0),若點P為C上一動點,且P點在x軸上方,當點P的位置變化時,△PAF的周長的最小值為_____.
,一個焦點為F(0,﹣8),則該雙曲線的標準方程為_____.已知點A(﹣6,0),若點P為C上一動點,且P點在x軸上方,當點P的位置變化時,△PAF的周長的最小值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】觀察不等式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 由此歸納第
由此歸納第![]() 個不等式為____________;要用數學歸納法證明該不等式,由
個不等式為____________;要用數學歸納法證明該不等式,由![]() 時不等式成立,推證
時不等式成立,推證![]() 時,左邊應增加的項數為____________.
時,左邊應增加的項數為____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:![]() 的焦點為F,直線y=4與y軸的交點為P,與C的交點為Q,且
的焦點為F,直線y=4與y軸的交點為P,與C的交點為Q,且![]() .
.
(1)求拋物線C的方程;
(2)過F的直線l與C相交于A,B兩點,若AB的垂直平分線![]() 與C相交于M,N兩點,且A,M,B,N四點在同一個圓上,求直線l的方程.
與C相交于M,N兩點,且A,M,B,N四點在同一個圓上,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,以等腰直角三角形斜邊BC上的高AD為折痕,把△ABD與△ACD折成互相垂直的兩個平面后,某學生得出下列四個結論:
①![]() ;
;
②∠BAC=60°;
③三棱錐D﹣ABC是正三棱錐;
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正確結論的序號是 .(請把正確結論的序號都填上)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com