
已知函數
(1)求 的單調區間和極值;
的單調區間和極值;
(2)若對于任意的 ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范圍
的取值范圍
(1) 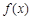 的單調增區間是
的單調增區間是 ,單調減區間是
,單調減區間是 和
和 ,當
,當 時,
時,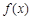 取極小值
取極小值 ,當
,當 時,
時,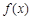 取極大值
取極大值 , (2)
, (2) 
解析試題分析:(1)求函數單調區間及極值,先明確定義域:R,再求導數 在定義域下求導函數的零點:
在定義域下求導函數的零點: 或
或 ,通過列表分析,根據導函數符號變化規律,確定單調區間及極值,即
,通過列表分析,根據導函數符號變化規律,確定單調區間及極值,即 的單調增區間是
的單調增區間是 ,單調減區間是
,單調減區間是 和
和 ,當
,當 時,
時, 取極小值
取極小值 ,當
,當 時,
時, 取極大值
取極大值 , (2)本題首先要正確轉化:“對于任意的
, (2)本題首先要正確轉化:“對于任意的 ,都存在
,都存在 ,使得
,使得 ”等價于兩個函數值域的包含關系.設集合
”等價于兩個函數值域的包含關系.設集合 ,集合
,集合 則
則 ,其次挖掘隱含條件,簡化討論情況,明確討論方向.由于
,其次挖掘隱含條件,簡化討論情況,明確討論方向.由于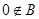 ,所以
,所以 ,因此
,因此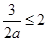 ,又
,又 ,所以
,所以 ,即
,即
解(1)由已知有 令
令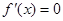 ,解得
,解得 或
或 ,列表如下:
,列表如下: