
【題目】計(jì)劃在某水庫建一座至多安裝4臺發(fā)電機(jī)的水電站,過去50年的水文資料顯示,水庫年入流量X(年入流量:一年內(nèi)上游來水與庫區(qū)降水之和,單位:億立方米)都在40以上,其中,不足80的年份有10年,不低于80且不足120的年份有30年,不低于120且不足160的年份有8年,不低于160的年份有2年,將年入流量在以上四段的頻率作為相應(yīng)段的概率,并假設(shè)各年的年入流量相互獨(dú)立.
(1)求在未來3年中,至多1年的年入流量不低于120的概率;
(2)水電站希望安裝的發(fā)電機(jī)盡可能運(yùn)行,但每年發(fā)電機(jī)最多可運(yùn)行臺數(shù)受年入流量X的限制,并有如下關(guān)系:
年入流量X |
|
|
|
|
發(fā)電機(jī)最多可運(yùn)行臺數(shù) | 1 | 2 | 3 | 4 |
若某臺發(fā)電機(jī)運(yùn)行,則該臺發(fā)電機(jī)年利潤為5000萬元;若某臺發(fā)電機(jī)未運(yùn)行,則該臺發(fā)電機(jī)年虧損1500萬元,水電站計(jì)劃在該水庫安裝2臺或3臺發(fā)電機(jī),你認(rèn)為應(yīng)安裝2臺還是3臺發(fā)電機(jī)?請說明理由.
【答案】(1)![]() ;(2)2臺,理由見解析
;(2)2臺,理由見解析
【解析】
(1)利用二項(xiàng)分布概率計(jì)算公式,求得至多![]() 年的年入流量不低于
年的年入流量不低于![]() 的概率.
的概率.
(2)分別求得安裝![]() 臺、
臺、![]() 臺發(fā)電機(jī)的利潤的期望值,由此確定安裝發(fā)動機(jī)的臺數(shù).
臺發(fā)電機(jī)的利潤的期望值,由此確定安裝發(fā)動機(jī)的臺數(shù).
(1)依題意:![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以年入流量不低于120的概率為![]()
由二項(xiàng)分布,在未來3年中,至多1年的年入流量不低于120的概率為:
![]() .
.
(2)記水電站的總利潤為![]() (單位:萬元)
(單位:萬元)
①若安裝2臺發(fā)電機(jī)的情形:
| 3500 | 10000 |
|
|
|
![]()
②若安裝3臺發(fā)電機(jī)的情形:
| 2000 | 8500 | 15000 |
|
|
|
|
![]()
因?yàn)?/span>![]() ,故應(yīng)安裝2臺發(fā)電機(jī).
,故應(yīng)安裝2臺發(fā)電機(jī).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙、丙三人參加微信群搶紅包游戲,規(guī)則如下:每輪游戲發(fā)![]() 個紅包,每個紅包金額為
個紅包,每個紅包金額為![]() 元,
元,![]() .已知在每輪游戲中所產(chǎn)生的
.已知在每輪游戲中所產(chǎn)生的![]() 個紅包金額的頻率分布直方圖如圖所示.
個紅包金額的頻率分布直方圖如圖所示.
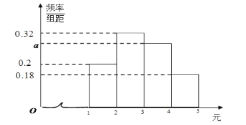
(1)求![]() 的值,并根據(jù)頻率分布直方圖,估計(jì)紅包金額的眾數(shù);
的值,并根據(jù)頻率分布直方圖,估計(jì)紅包金額的眾數(shù);
(2)以頻率分布直方圖中的頻率作為概率,若甲、乙、丙三人從中各搶到一個紅包,其中金額在![]() 的紅包個數(shù)為
的紅包個數(shù)為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)生對函數(shù)![]() 的性質(zhì)進(jìn)行研究,得出如下的結(jié)論:
的性質(zhì)進(jìn)行研究,得出如下的結(jié)論:
![]() 函數(shù)在
函數(shù)在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增;
上單調(diào)遞增;
![]() 點(diǎn)
點(diǎn)![]() 是函數(shù)圖象的一個對稱中心;
是函數(shù)圖象的一個對稱中心;
![]() 函數(shù)圖象關(guān)于直線
函數(shù)圖象關(guān)于直線![]() 對稱;
對稱;
![]() 存在常數(shù)
存在常數(shù)![]() ,使
,使![]() 對一切實(shí)數(shù)x均成立,
對一切實(shí)數(shù)x均成立,
其中正確命題的個數(shù)是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列各命題中正確命題的序號是( )
① “若![]() 都是奇數(shù),則
都是奇數(shù),則![]() 是偶數(shù)”的逆否命題是“
是偶數(shù)”的逆否命題是“![]() 不是偶數(shù),則
不是偶數(shù),則![]() 都不是奇數(shù)”;
都不是奇數(shù)”;
② 命題“![]() ”的否定是“
”的否定是“![]() ” ;
” ;
③ “函數(shù)![]() 的最小正周期為
的最小正周期為![]() ” 是“
” 是“![]() ”的必要不充分條件;
”的必要不充分條件;
④“平面向量![]() 與
與![]() 的夾角是鈍角”的充分必要條件是“
的夾角是鈍角”的充分必要條件是“![]() ”
”
A. ①②B. ③④C. ②③D. ②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 邊的中點(diǎn),以
邊的中點(diǎn),以![]() 為折痕把
為折痕把![]() 折起,使點(diǎn)
折起,使點(diǎn)![]() 到達(dá)點(diǎn)
到達(dá)點(diǎn)![]() 的位置,且
的位置,且![]() .
.
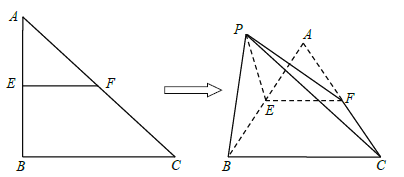
(1)證明:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在五面體![]() 中,側(cè)面
中,側(cè)面![]() 是正方形,
是正方形,![]() 是等腰直角三角形,點(diǎn)
是等腰直角三角形,點(diǎn)![]() 是正方形
是正方形![]() 對角線的交點(diǎn)
對角線的交點(diǎn)![]() ,
,![]() 且
且![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)若側(cè)面![]() 與底面
與底面![]() 垂直,求五面體
垂直,求五面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=|x+1|+2|x﹣m|
(1)當(dāng)m=2時,求f(x)≤9的解集;
(2)若f(x)≤2的解集不是空集,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)設(shè)![]() 為
為![]() 上的一點(diǎn),滿足
上的一點(diǎn),滿足![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com